Die CS4272 ist ein hochwertiges Stereo Audio-CODEC von Cirrus Logic für anspruchsvolle Implementierungen. Es unterstützt 24bit Bittiefe, bis zu 192kHz Abtastrate und besitzt einen dynamischen Bereich vom 114dB.
Für Flex 500 wurde ein Breakout-Board für CS4272 entwickelt, das man direkt auf ein Nucleo Board stecken kann.

PCB Design

CS4272 CODEC- Breakout board im Betrieb
Board-Design
CS4272 unterstützt 2x symmetrische Eingänge und hat 2x symmetrische Ausgänge.
Symmetrische Eingänge
Die Nutzsignale vom analogen Preamp-Board sind Wechselspannungen, da Preamp-Board symmetrische Spannungsversorgung von ![]() hat. Für die symmetrischen Eingänge muss das Signal vom Preamp-Board in einen Pegel von
hat. Für die symmetrischen Eingänge muss das Signal vom Preamp-Board in einen Pegel von ![]() gebracht werden. Danach muss eine Gleichspannung
gebracht werden. Danach muss eine Gleichspannung ![]() addiert werden, damit das Eingangssignal in den erlaubten Bereich vom CS4272
addiert werden, damit das Eingangssignal in den erlaubten Bereich vom CS4272 ![]() gebracht werden. Das wird in der untenstehenden Schaltung realisiert:
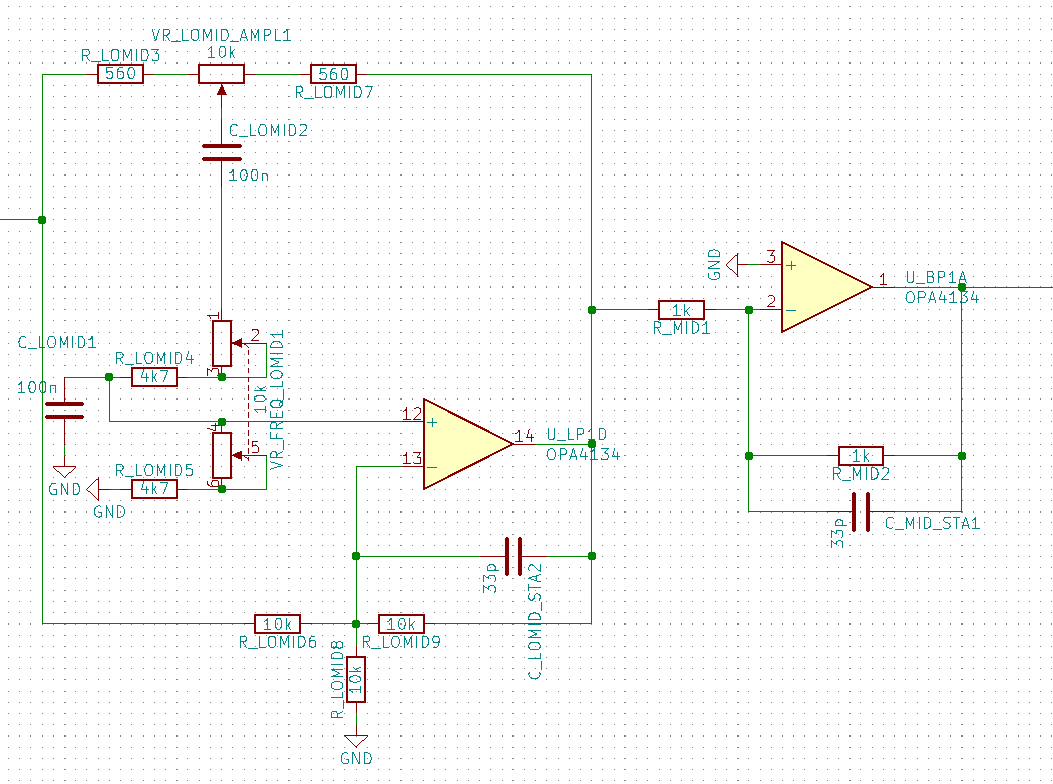
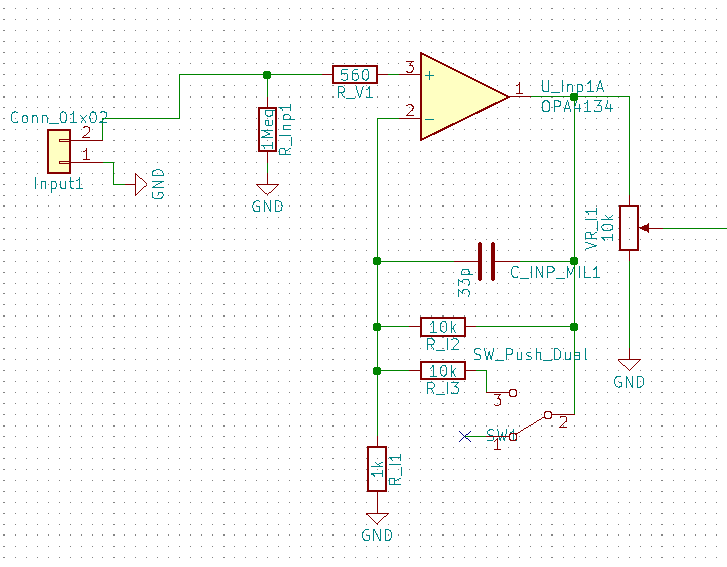
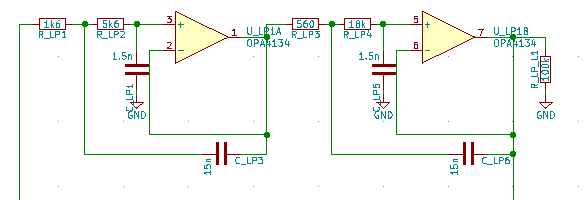
gebracht werden. Das wird in der untenstehenden Schaltung realisiert:

Bei diesem Design handelt es sich um das Referenzdesign von CS4272. Hierbei wird die Alias-Spannung ![]() auf die durch die Kondensatoren C_INAx entkoppelte Eingangsspannung addiert und ein Eingangspuffer hinzugefügt.
auf die durch die Kondensatoren C_INAx entkoppelte Eingangsspannung addiert und ein Eingangspuffer hinzugefügt.
Symmetrische Ausgänge
Die analogen Ausgänge vom CS4272 symmetrisch und für weitere Verarbeitung desymmetriert werden. Das wurde mit folgender Schaltung realisiert.
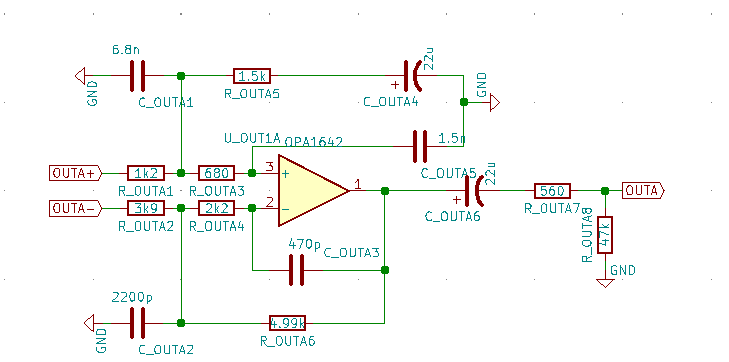
Hierbei werden die symmetrischen Signale ![]() und
und ![]() in einer Stufe voneinander abgezogen. Danach wird mit dem Ausgangskondesator C_OUTA6 der Gleichstrom herausgefiltert. Schließlich arbeitet die ganze Schaltung auf einen Lastwiderstand von
in einer Stufe voneinander abgezogen. Danach wird mit dem Ausgangskondesator C_OUTA6 der Gleichstrom herausgefiltert. Schließlich arbeitet die ganze Schaltung auf einen Lastwiderstand von ![]() . Hierbei handelt es sich um das Referenz Design von CS4272.
. Hierbei handelt es sich um das Referenz Design von CS4272.
Digitale Schnittstellen
Das Breakout-Board unterstützt SPI und I2C Schnittstellen zum Controller.
Initialisierungssequenz
Die Initialisierungssequenz von CS4272 ist im folgenden Code gezeigt.
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 58 59 60 61 |
void cs4272::init(void){ //Initialize SPI printf("Initing SPI5\n"); MX_SPI5_Init(); printf("Initing codec\n"); HAL_GPIO_WritePin(GPIOG,GPIO_PIN_0,(GPIO_PinState)0); //RST low uint8_t i=0; uint8_t reg[8][3]; uint8_t adr=0b00100000; //Init address for(i=0;i<sizeof(reg)/3;i++){ reg[i][0]=adr; } //Define startup sequence reg[0][1]=0x7; //Power down control reg[0][2]=0b00000011; //Set Serial mode + power down reg[1][1]=0x1; //Mode control 1 reg[1][2]=0b00101001; //48kHz Master reg[2][1]=0x2; //DAC Control reg[2][2]=0b00000000; reg[3][1]=0x3; //DAC Volume control reg[3][2]=0b00001001; reg[4][1]=0x4; //DAC Volume A reg[4][2]=0b10000000; //No mute + 0dB reg[5][1]=0x5; //DAC Volume B reg[5][2]=0b10000000; //No mute + 0dB reg[6][1]=0x6; //ADC Control reg[6][2]=0b00010000; reg[7][1]=0x7; //Mode control 2 reg[7][2]=0b00001010; // reg[7][2]=0b00010010;//Loop ADC->DAC HAL_GPIO_WritePin(GPIOG,GPIO_PIN_1,(GPIO_PinState)1); //MS high: SPI Unselect device HAL_GPIO_WritePin(GPIOG,GPIO_PIN_0,(GPIO_PinState)1); //RST High HAL_Delay(2); //Wait //HAL_GPIO_WritePin(GPIOG,GPIO_PIN_0,0); //RST Low for(i=0;i<sizeof(reg)/3;i++){ HAL_GPIO_WritePin(GPIOG,GPIO_PIN_1,(GPIO_PinState)0); //MS low: SPI Select device HAL_SPI_Transmit(&hspi5,(uint8_t *)®[i],3,1000); //Send config register HAL_GPIO_WritePin(GPIOG,GPIO_PIN_1,(GPIO_PinState)1);//MS high: SPI Unselect device HAL_Delay(1); //Wait } } |
Nach der Initialisierung kann das CODEC aktiviert und deaktiviert werden.
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 |
void cs4272::set_status(bool flag){ uint8_t mutereg[3]; mutereg[0]=0b00100000; mutereg[1]=0x4; //DAC Volume control A register (MUTECA=B is on) if(flag){ mutereg[2]=0b00000000; }else{ mutereg[2]=0b10000000; } //Send SPI command to CODEC HAL_GPIO_WritePin(GPIOG,GPIO_PIN_1,(GPIO_PinState)0); //MS low: SPI Select device HAL_SPI_Transmit(&hspi5,(uint8_t *)&mutereg,3,1000); //Send config register HAL_GPIO_WritePin(GPIOG,GPIO_PIN_1,(GPIO_PinState)1);//MS high: SPI Unselect device } |
Der SAI von H743 muss folgendermaßen konfiguriert sein:
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 |
void c_sai::MX_SAI1_Init(void) { hsai_BlockA1.Instance = SAI1_Block_A; hsai_BlockA1.Init.AudioMode = SAI_MODESLAVE_RX; hsai_BlockA1.Init.Synchro = SAI_ASYNCHRONOUS; hsai_BlockA1.Init.OutputDrive = SAI_OUTPUTDRIVE_DISABLE; hsai_BlockA1.Init.FIFOThreshold = SAI_FIFOTHRESHOLD_EMPTY; hsai_BlockA1.Init.AudioFrequency = SAI_AUDIO_FREQUENCY_48K; hsai_BlockA1.Init.SynchroExt = SAI_SYNCEXT_OUTBLOCKA_ENABLE; hsai_BlockA1.Init.MonoStereoMode = SAI_STEREOMODE; hsai_BlockA1.Init.CompandingMode = SAI_NOCOMPANDING; hsai_BlockA1.Init.TriState = SAI_OUTPUT_NOTRELEASED; if (HAL_SAI_InitProtocol(&hsai_BlockA1, SAI_I2S_STANDARD, SAI_PROTOCOL_DATASIZE_32BIT, 2) != HAL_OK) { // _Error_Handler(__FILE__, __LINE__); } hsai_BlockB1.Instance = SAI1_Block_B; hsai_BlockB1.Init.AudioMode = SAI_MODESLAVE_TX; hsai_BlockB1.Init.Synchro = SAI_SYNCHRONOUS; hsai_BlockB1.Init.OutputDrive = SAI_OUTPUTDRIVE_DISABLE; hsai_BlockB1.Init.FIFOThreshold = SAI_FIFOTHRESHOLD_EMPTY; hsai_BlockB1.Init.SynchroExt = SAI_SYNCEXT_DISABLE; hsai_BlockB1.Init.MonoStereoMode = SAI_STEREOMODE; hsai_BlockB1.Init.CompandingMode = SAI_NOCOMPANDING; hsai_BlockB1.Init.TriState = SAI_OUTPUT_NOTRELEASED; if (HAL_SAI_InitProtocol(&hsai_BlockB1, SAI_I2S_STANDARD, SAI_PROTOCOL_DATASIZE_32BIT, 2) != HAL_OK) { // _Error_Handler(__FILE__, __LINE__); } } void c_sai::start(void){ //Start DMA Streams printf("Initializing SAI DMA Receive stream...\n"); // printf("Initializing SAI DMA Receive stream...\n"); HAL_SAI_Receive_DMA(&hsai_BlockA1, (uint8_t*)&rx_buf, 4*buf_size); printf("SAI DMA Receive stream initialized!\n"); // printf("Initializing SAI DMA transmit stream...\n"); HAL_SAI_Transmit_DMA(&hsai_BlockB1, (uint8_t*)&tx_buf, 4*buf_size); printf("SAI DMA transmit stream initialized!\n"); } |
Oszillator
Ein 24,576 MHz Oszillator ist eingebaut und gibt den Takt an den Master-Clock.
Ressourcen
SPICE-Simulationsdateien zu analogen Schnittstellen für CS4272 herunterladen




![Rendered by QuickLaTeX.com \begin{equation*} \begin{aligned} g&=\frac{g_{max}}{9} [ 10^{v/100}-1] \\ x& \in \{0 ... 100\} \end{aligned} \end{equation*}](https://www.cankosar.com/wp-content/ql-cache/quicklatex.com-efe59a3430cbbbc5fb148600a18f7b33_l3.png)