Nachdem die Frequenz ermittelt wurde, muss nun dem Anwender dargestellt werden, welche Soll-Note erkannt wurde und wieviel die berechnete Ist-Note von der Soll-Note abweicht, damit dieser sein Instrument stimmen kann.
Abschätzung der Soll-Note
Dabei wird gesucht, welcher Notenfrequenz, die gemessene Frequenz am nächsten ist. Da die Frequenzskala logarithmisch ist, müssen die Schranken von einzelnen Noten bestimmt werden, die von der Hauptfrequenz +-50 cent entfernt sind.
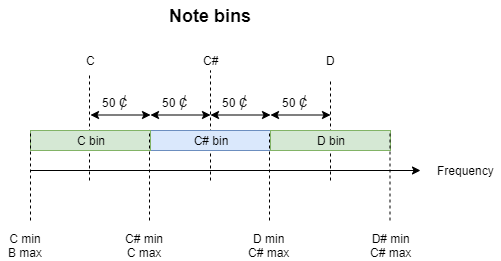
Berechnung der Schranken
Die Schranken, die 50 cent von der Hauptfrequenz entfernt sind, werden zunächst einmalig berechnet. Wenn sich die Kammertonfrequenz 
(z.B. A4=440Hz) ändert, müssen die Schranken wieder berechnet werden, aber nicht in jedem Messzyklus.
Die Frequenzen der Hauptnoten berechnen sich als
(1) 
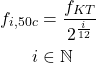
Dann können wir die 50 cent verschobene Frequenzen als
(2) 
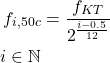
berechnen.
Die Implementierung kann folgendermaßen realisiert werden:
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 |
void c_tuner::init(void){ //12th root of 2 must be calculated once root2_12=pow((double) 2,(double) 1/12); } void c_tuner::update_note_bins(double freq_A4){ notes[0]=((double) freq_A4 / (double)16); note_bins[0]= notes[0] * pow((double) 2,(double) -1/24); //A0 + 50cents uint8_t i; for(i=1;i<num_notes;i++){ note_bins[i]=(double) note_bins[i-1]*root2_12; notes[i]=(double) notes[i-1]*root2_12; } } |
Suche nach den Schranken
Dafür eignet sich der binäre Suchalgorithmus, wenn wir keine Vorschätzung haben. Falls wir eine Vorschätzung haben (ein guter Ansatz ist die letzte gemessene Schranke zu nehmen) eignet sich auch die lineare Suche.
Im folgenden ist die Implementierung mit einem modifizierten binären Suchalgorithmus gezeigt.
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 |
/*Modified binary search*/ uint8_t c_tuner::find_note_index(double freq){ // printf("Note %f\n",freq); //Declaration uint8_t l,r,c; //Start values l=0; r=num_notes; c=floor((l+r)/2); //Binary search algorithm while((r-l)>1){ if(freq>=note_bins[c]){ l=c; }else{ r=c; } c=floor((l+r)/2); } return c; } |
Berechnung der Abweichung
Die Abweichung von der Soll-Note kann folgendermaßen berechnet werden.
|
1 2 3 4 5 6 |
/*Calculate cent*/ double c_tuner::calculate_cent(double f, double fr){ //Calculate cents return 1200*log2(f/fr); } |
Für die Zuordnung des Notenindex zur Notenbezeichnung ist ein String-Array hinterlegt.
|
1 |
const char *s_notes[12] = {"A","A#","B","C","C#","D","D#","E","F","F#","G","G#"}; |
Der gesamte Ablauf der Notenfindung sieht also folgendermaßen aus.
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 |
//Calculate note and update actual note register void c_tuner::calculate_note(double freq){ //Declarations uint8_t note_index; //Get the note bin (lower border) note_index = find_note_index(freq); //Get the name of the note act_note=s_notes[note_index%12]; //Calculate the deviation of the current frequency from the aimed note in cents act_cent=calculate_cent(freq,notes[note_index]); // printf("f:%.2f \t [%.2f - %.2f] \t %s %f\n",(float)freq, note_bins[note_index],note_bins[note_index+1],act_note,act_cent); } |
Ressourcen
Vollständigen Target-Code der Tuner-Anzeige vom Github herunterladen.
Schreibe einen Kommentar