Die Dynamikkompression (engl. Dynamic range compression) ist ein Prozess, der die Dynamik komprimiert bzw. reduziert. Das wird gemacht, indem die lauten Bereiche, die einen Schwellwert überschreiten, leiser gemacht werden, während die leiseren Bereiche unreduziert passieren. Die Charakteristik der Kompression lässt sich am Besten in einer Dynamikkurve darstellen, die die Beziehung zwischen der Einganglautstärke und Ausgangslautstärke beschreibt.
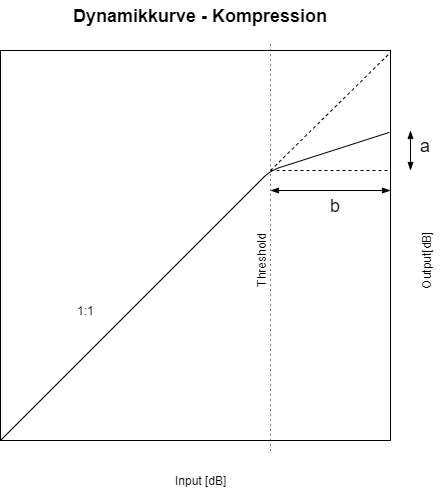
Die Steigung 
beschreibt die Kompressionsrate, mit der das Signal abgeschwächt wird. Dies greift ab dem Überschreiten eines Threshold-Werts.
Digitale Realisierung
Das Herzstück eines Kompressors ist ein spannungskontrollierter Verstärker (VCA). Im analogen Design, wird das mit komplexen Schaltungen realisiert. In der Digitaltechnik ist dies ein simpler Verstärkungsfaktor, mit dem das Signal multipliziert wird. Dieser Verstärkungsfaktor wird in einem parallelen Pfad berechnet. Der parallele Pfad besteht aus einem Lautstärkendetektor (in der Regel realisiert mit Effektivleistung, RMS) und einer Logik, die die Reduktion aus der Lautstärke berechnet (Gain computer).
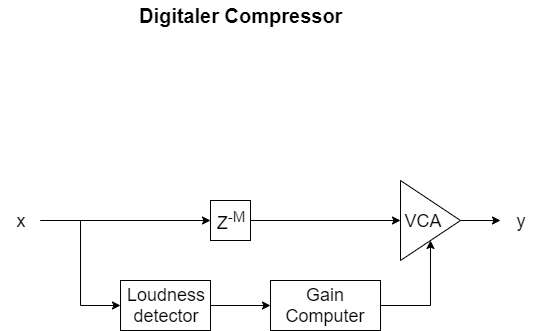
Loudness detector
Einer der wichtigsten Bestandteile einer Kompression ist die Berechnung der Lautstärke, Hier wird kontinuierlich ermittelt, wie hoch die empfundene Lautstärke ist. Gängigste Methode dafür ist der Effektivwert als quadratischer Mittelwert des relevanten Sampleabschnitts.
(1) 
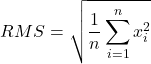
Der RMS-Wert dient als Eingang für den Gain-Computer. Der Gain-Computer berechnet daraus die Verstärkung, die dem Signal appliziert werden soll. Es appliziert die Dynamikkurve, s. oben.
Parameter
Folgende Kontrollparameter sind für einen Kompressor Effekt üblich:
Input gain
Die Eingangsverstärkung wird auf das Eingangssignal appliziert, um das Signalniveau in einen gewünschten Platz in der Dynamikkurve zu platzieren. Alternativ kann man auch Threshold verschieben.
Threshold
Der Threshold (dt. für Schranke/Grenze) ist der Grenzwert, ab dessen Überschreitung eine Gain-Reduktion erfolgt, s. Diagramm.
Kompressionsrate
Sie beschreibt die Stärke der Gain-Reduktion nach Threshold, in der Dynamikkurve ist dies als Tangenzwert gezeigt.
Ab einem Wert von 60:1 wird von einem Limiter gesprochen.
Make-Up Gain
Der Gain-Computer appliziert eine Gain-Reduktion. Das bedeutet, die gesamte Lautstärke des Signals sinkt. Um das ältere Lautstärkenniveau zu erreichen, wird ein Make-Up Gain am Ausgang appliziert.
Soft-Knee / Hard-Knee
Ab dem Threshold ändert sich die Verstärkung, die man appliziert. Dieser Übergang, der in der Dynamikkurve oben scharf gezeichnet wurde, kann auch mild erfolgen. So dass die Gain-Reduktion langsam eintritt.
Attack
Der Attack-Wert bestimmt, wann die Gain-Reduktion nach einer Überschreitung eintreten soll. Sie liegt im Bereich von 5 bis 250 ms.
Release
Der Release-Wert bestimmt, wann nach einer Unterschreitung des Tresholds die Gain-Reduktion wieder aussetzen soll. Sie liegt üblicherweise im Bereich von 5 bis 100ms.
Implementierung
Im folgenden ist die Prozessroutine eines Kompressors gezeigt:
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 58 59 60 61 62 63 64 65 66 67 68 69 70 71 72 73 74 75 76 77 78 79 80 81 82 83 84 85 86 87 88 89 90 91 92 93 94 95 96 97 |
/* Compressor main process */ float c_compressor::process(float x){ x*=input_gain; //Calculate RMS //Subtract oldest the value (rmsbuf[rptr]) from the sum rms_sum-=(rmsbuf[rptr]*rmsbuf[rptr])/(float)rms_len; //Add the newest value to the sum rms_sum+=(x*x)/rms_len; if(rms_sum<0){ printf("Warning: RMS sum negaive %f\n",rms_sum); rms_sum=0; } //Update the RMS Value c_rms=fast_sqroot(rms_sum); //Get logarithmic value c_rms=fast_log2(c_rms); //Update the buffer rmsbuf[rptr]=x; //Increment rptr++; if(rptr>=rms_len){ rptr=0;; } //Update main buf //Output is the last value on the buffer float y; y=buf[ptr]; //Set the new value to the buffer buf[ptr]=x; //Increment ptr++; if(ptr>=delay_len){ ptr=0;; } //Calculating attenuation float exponent; if(c_rms>threshold){ //Calculating exponent according Udo Zölzer exponent=-1*(c_rms-threshold)*slope; //Exponents smaller than -1500 are making fast algorithms unstable if(exponent<-100){ target_gain=0; }else{ target_gain=fastPow(2,exponent); // target_gain=pow(2,exponent); } }else{ target_gain=1; } //Attack and release if(comp_gain>target_gain){ //Attack comp_gain-=stepsize_attack; //Break decreasing if(comp_gain<=target_gain){ comp_gain=target_gain; } }else{ //Release comp_gain+=stepsize_release; //Break increasing if(comp_gain>=1){ comp_gain=1; } } return y*comp_gain;; } |
Quadratwurzel (Root square) Implementierung
Eine der wichtigsten Komponenten des Kompressors ist der RMS-Rechner. Der Aufwand der Berechnung der Quadratsumme ist eine Multiplikation und eine Addition. Hingegen ist die Quadratwurzelberechnung eine sehr aufwändige Berechnung, die den Flaschenhals darstellt. Hierzu gibt es effiziente Algorithmen, die dies übernehmen. Ein davon (hier eingesetzter) Algorithmus ist der berühmte „fastsqroot„-Algorithmus. Dieser Algorithmus ist ursprünglich für Videoverarbeitung entwickelt und mittlerweile gut analysiert und breit eingesetzt.
|
1 2 3 4 5 6 7 8 9 |
inline double fastPow(double a, double b) { union { double d; int x[2]; } u = { a }; u.x[1] = (int)(b * (u.x[1] - 1072632447) + 1072632447); u.x[0] = 0; return u.d; }; |
Potenzimplementierung
Der berechnete RMS-Wert wird in einen logarithmischen Wert umgerechnet, woraus sich die wahrgenommene Lautstärke 
ergibt. Jeder Mensch empfindet die Lautstärke anders. Mann kann den Logarithmus auf 2 Basis, 10 Basis oder natürlichen Logarithmus nehmen.
(2) 
Die Potenzberechnung der Gleitkommazahlen ist auch eine teure Operation. Die Funktion pow() der Mathe-Bibliothek ist selbst auf FPUs sehr langsam, da es für alle Zahlen eine gute Genauigkeit liefern muss. Wir brauchen aber keine sehr Hohe Genauigkeit, da wir nur ein Verstärkungsfaktor berechnen. Dafür gibt es schnellere Funktion, wie z.B. fastPow
|
1 2 3 4 5 6 7 8 9 |
inline double fastPow(double a, double b) { union { double d; int x[2]; } u = { a }; u.x[1] = (int)(b * (u.x[1] - 1072632447) + 1072632447); u.x[0] = 0; return u.d; }; |
Klangbeispiele
Den Klang eines Kompressors sollte man im Optimalfall nicht hören. Dennoch hier ein paar Beispiele der sehr starken Komprimierung, wo die Kompression im Vergleich zum trockenen Signal erkennbar ist.
Schreibe einen Kommentar