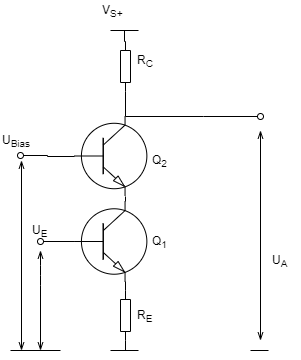
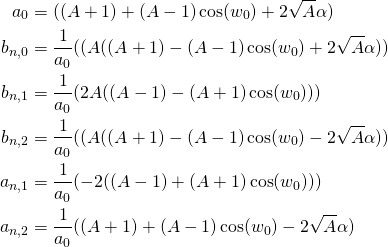Die erste Stufe eines Class A / AB Verstärkers ist ein Differenzverstärker. Auch die Eingangsstufe und das Herzstück der Operationsverstärker sind Differenzverstärker (Differential amplifier), da diese üblicherweise auf Class AB – Architektur basieren. Die Hauptfunktion der Differenzverstärker ist das Subtrahieren von zwei Signalen. Bei einem Closed-Loop-Verstärker ist der Differenzverstärker die Komponente, die die Fehler der nachfolgenden Spannungs- und Stromverstärkungssstufen kompensiert. Deshalb ist die Qualität der Differenzverstärkerstufe maßgeblich für die Qualität des gesamten Verstärkers.
Es gibt u. a. zwei grundsätzliche Möglichkeiten, einen Differenzverstärker realisieren:
- Differenzverstärker mit bipolaren Transistoren (BJT)
- Differenzverstärker mit Feldeffekt-Transistoren (FET)
Der Vorteil beim Aufbau mit bipolaren Transistoren ist, dass diese recht unempfindlich für die thermischen Auswirkungen sind. Dafür haben diese aber einen niedrigen Eingangsimpedanz.
Der Vorteil der FETs sind, dass diese sehr hohen Eingangsimpedanz besitzen und dadurch besser für die Verstärkung kleinerer Signale bzw. Ströme eignen. Beim Aufbau der (guten) Operationsverstärker sind deshalb verbreiteter. Der Hauptnachteil der FETs besteht darin, dass diese eine große Streuung bei thermischen Eigenschaften besitzen. Dadurch sind die FET-Differenzverstärkern für diskreten Aufbau eher ungeeignet, da es schwieriger ist, die thermischen Ungleichheiten beider FETs auszugleichen. Auf integrierten Schaltungen sind diese Effekte viel besser beherrschbar, da v. a. die Transistoren in demselben Chip sind, wo die thermischen Effekte gleichmäßiger sind.
Um die negativen Einflüsse der thermischen Effekte zu reduzieren, werden bei einem diskreten Aufbau beide Transistoren des Differenzverstärker physisch nah realisiert. Dadurch wird versucht, dass die thermischen Effekte zumindest auf beide Transistoren wirken und kompensiert werden.
Funktionsprinzip der beiden Varianten ist gleich. Da diese Artikelserie sich auf den diskreten Aufbau der Schaltungen basiert, werden im folgenden die Differenzverstärker mit bipolaren Transistoren erläutert.
Funktionsprinzip
Wenn an beiden Eingängen die gleiche Spannung anliegt, ist sind die Ströme und somit Kollektorspannungen an beiden Zweigen gleich . Dadurch entsteht keine Spannungsdifferenz an beiden Kollektoren. Somit gilt 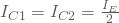 .
.
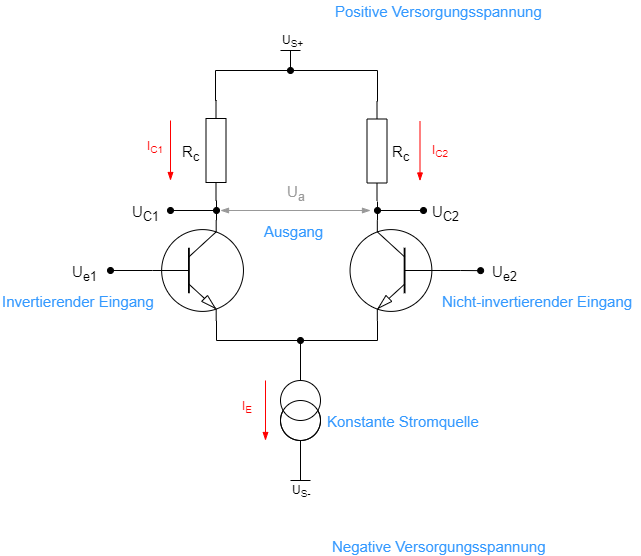
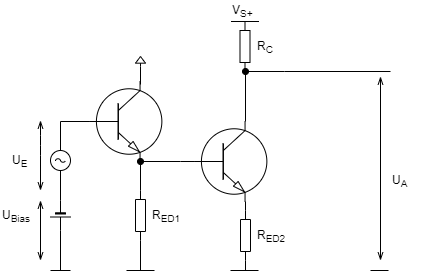
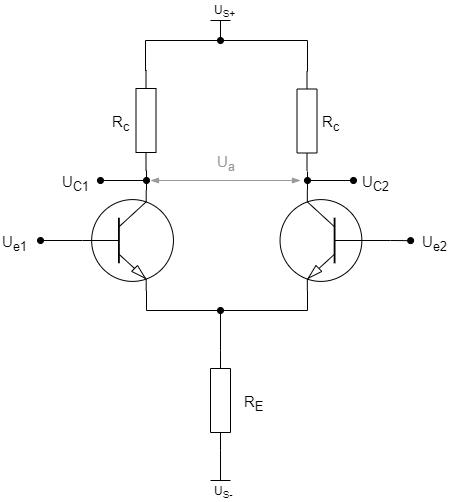
Eine Vereinfachung der Konstantstromquelle ist ein Widerstand. D.h. eine funktionierende Schaltung würde so aussehen.
Dimensionierung
1. Arbeitsstrom 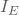 der Stromquelle festlegen
der Stromquelle festlegen
Hier spielen u. a. zwei wichtige Faktoren eine Rolle:
a) Die Differenzstufe eines Verstärkers steuert eine Spannungsverstärkungsstufe. Man kann sich vorstellen, dass die Ausgangsimpedanz des Differenzverstärkers mit der Eingangsimpedanz des Spannungsverstärkers parallelgeschaltet sind. Daher muss die Ausgangsimpedanz des Differenzverstärkers möglichst niedrig (und die Eingangsimpedanz des Spannungsverstärkers möglichst hoch) sein, damit der Differenzverstärkungsfaktor möglichst hoch bzw. der Klirrfaktor möglichst niedrig bleibt. Dies erfordert einen möglichst hohen Arbeitsstrom.
b) Die Transistoren müssen mit möglichst niedrigen Strömen arbeiten, damit der Einfluss der thermischen Effekte reduziert wird. Zudem ermöglichen niedrige Ströme bessere Energieeffizienz.
Unter Berücksichtigung dieser Aspekte kann ein Arbeitsstrom 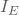 festgelegt werden. Bei einem Spannungsverstärker mit hoher Eingangsimpedanz ermöglicht ein Arbeitsstrom von
festgelegt werden. Bei einem Spannungsverstärker mit hoher Eingangsimpedanz ermöglicht ein Arbeitsstrom von 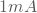 bis
bis 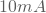 eine gute Ausgangsimpedanz und ist dennoch thermisch effizient.
eine gute Ausgangsimpedanz und ist dennoch thermisch effizient.
2. Kollektorspannung am Arbeitspunkt festlegen
Bei den Audiosignalen geht es um Wechselspannungen. Daher kann man den Arbeitspunkt als 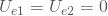 definieren. Die Kollektorspannungen der NPN-Transistoren schwanken zwischen
definieren. Die Kollektorspannungen der NPN-Transistoren schwanken zwischen 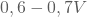 und
und 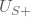 Um eine gute Aussteuerbarkeit zu haben, sollte die Spannung am Arbeitspunkt
Um eine gute Aussteuerbarkeit zu haben, sollte die Spannung am Arbeitspunkt 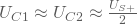 betragen. Bei einem einfachen Widerstand als Stromquelle lässt sich das mit
betragen. Bei einem einfachen Widerstand als Stromquelle lässt sich das mit 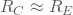 realisieren. Dadurch kann der Emitterwiderstand
realisieren. Dadurch kann der Emitterwiderstand  sowohl rechnerisch als auch simulativ berechnet werden.
sowohl rechnerisch als auch simulativ berechnet werden.
3. Konstantstromquelle realisieren
Es gibt verschiedene Möglichkeiten, eine Konstantstromquelle zu realisieren, die verschiedene Güte, Aufwand und Komplexität haben. Man kann die Konstantstromquellen ebenso diskret wie durch ICs realisieren. Die einfachste Form von einem einzelnen Widerstand ist für anspruchsvolle Audio-Zwecke nicht ausreichend. Doch mit Hilfe weniger Halbleitern können Stromquellen ausreichender Qualität gebaut werden. Im folgenden ist eine sehr verbreitete Stromquelle gezeigt, die in vielen anspruchsvollen Anwendungen zu finden ist.
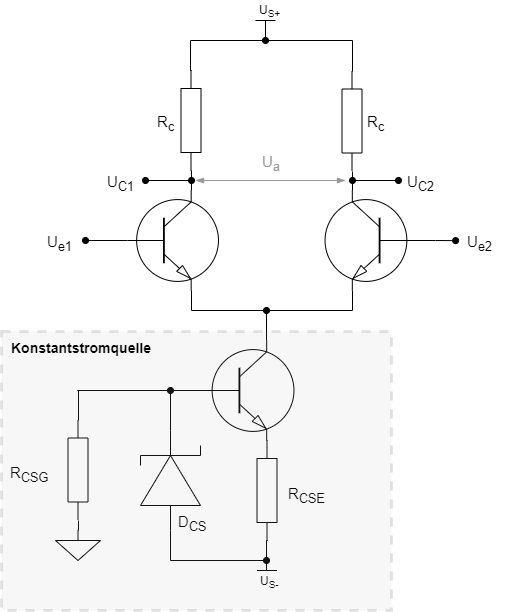
Erweiterung durch Stromspiegel
Die obige Schaltung basiert auf den symmetriebedingten Ähnlichkeit der Kollektorströme durch die gleichen Kollektorwiderstände 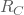 . Dies kann durch einen Stromspiegel (engl. current mirror) ersetzt werden, um eine aktive Regelung der Kollektorströme
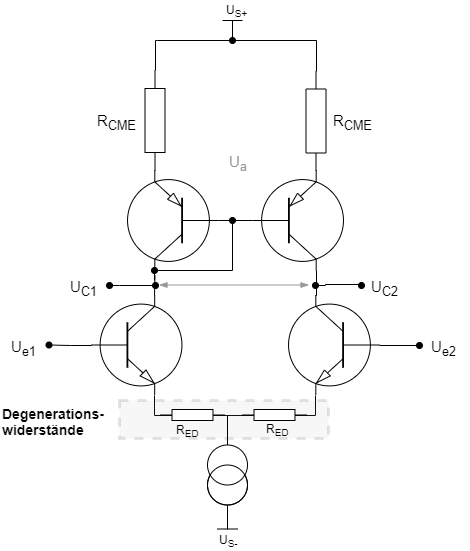
. Dies kann durch einen Stromspiegel (engl. current mirror) ersetzt werden, um eine aktive Regelung der Kollektorströme 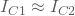 , und dadurch eine deutlich höhere Differenzverstärkung zu erzielen. So kann die obige Schaltung folgendermaßen erweitert werden:
, und dadurch eine deutlich höhere Differenzverstärkung zu erzielen. So kann die obige Schaltung folgendermaßen erweitert werden:
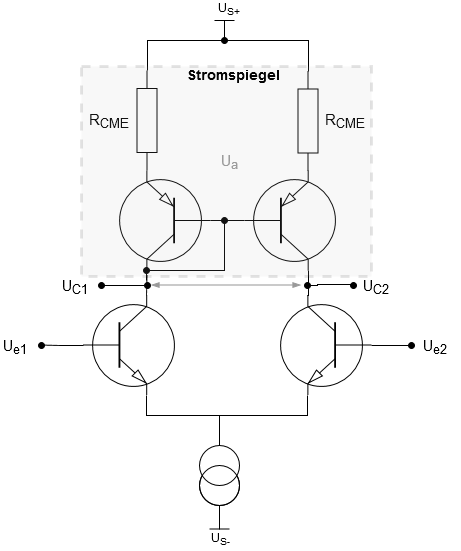
Durch die Erweiterung durch Stromspiegel geht allerdings die Symmetrie am Ausgang verloren und es entsteht ein Offset. Dies wird aber im geschlossenen Regelkreis (Closed-Loop) des Verstärkers herausgeregelt.
Degenerationswiderstand am Emitter
Transkonduktanz
Bei der Common-Emitter-Konfiguration ist die Transkonduktanz eine wichtige Größe und definiert das Verhältnis zwischen Basis-Emitterspannung und des Kollektorstroms. Bei einem bipolaren Transistor wird aber der Kollektorstrom durch die Basis-Emitterspannung geregelt. D.h. wenn die Basis-Emitter-Spannung erhöht wird, erhöht sich auch die Transkonduktanz. Das ergibt ein exponentielles Verhältnis zwischen der Basis-Emitter-Spannung und und dem Kollektorstrom. Transkonduktanz kann als
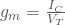
definiert werden. Ein typischer Wert für die thermale Spannung ist 26mV im Raumtemperatur. Die inverse Transkondukanz kann auch als ein effektiver dynamischer Emitterwiderstand 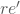 vorgestellt werden, dessen Wert vom Kollektorstrom abhängt.
vorgestellt werden, dessen Wert vom Kollektorstrom abhängt.
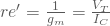
D.h. zusammengefasst, bei einer normalen Common-Emitter-Konfiguration ist die Verstärkung nicht linear. Je größer die Verstärkung, desto höher ist der Stromdurchlass durch den Kollektor und dadurch ergibt eine Art Verzerrung (engl. degeneration).
Um diese Verzerrung zu reduzieren, kann dieser virtuelle Emitterwiderstand 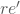 mit einem weiteren Emitterwiderstand erweitert werden. bei einem zusätzlichen Widerstand von
mit einem weiteren Emitterwiderstand erweitert werden. bei einem zusätzlichen Widerstand von 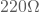 wird die Degeneration um ungefähr um das 10-fache verbessert. Im Gegenzug wird die (Open-Loop) Verstärkung der Common-Emitter-Konfiguration auf ein zehntel reduziert.
wird die Degeneration um ungefähr um das 10-fache verbessert. Im Gegenzug wird die (Open-Loop) Verstärkung der Common-Emitter-Konfiguration auf ein zehntel reduziert.
Simulation der Differenzverstärker
Die Differenzverstärker liefern je nach Bauart üblicherweise sehr hohe Open-Loop-Verstärkungen und sind üblicherweise als Subtrahierer in geschlossenen Regelkreisen eingesetzt. Bei der Open-Loop-Simulation muss deshalb beachtet werden, dass sich die Differenzverstärker nur in einem kleinen Bereich der Eingangsspannungen linear verhält. Bei der Verstärkung großer Spannungsdifferenzen ist dieser deshalb schnell gesättigt und nichtlinear. Anbei befinden sich LT-Spice-Simulationen der oben vorgestellten Varianten.
LTSPICE-Datei herunterladen
Nachweise / Literatur
Eine ausführliche Schaltungsanalyse, Klirrfaktoranalyse und die Herleitungen der bipolaren und FET-Differenzverstärker sind u. a. unter
https://home.zhaw.ch/kunr/Elektronik/Skript_MVKuenzli_ab%20SS04/Kap_9.pdf
zu finden. Zudem siehe
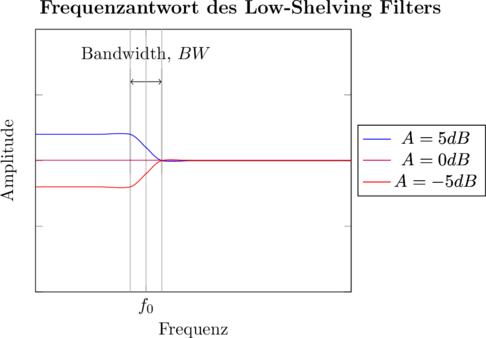
![]() , während es den Rest des Spektrums durchlässt.
, während es den Rest des Spektrums durchlässt.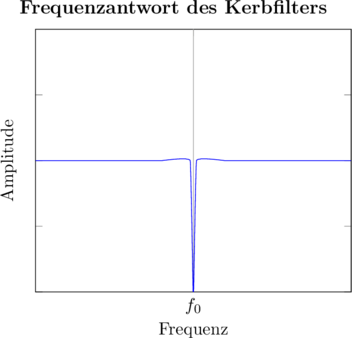
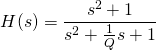
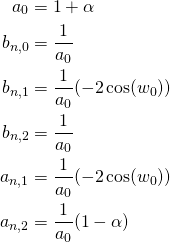
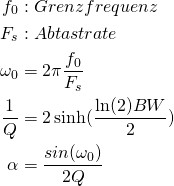
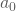 zu teilen, wird mit inversem (ein mal vorberechneten) Wert
zu teilen, wird mit inversem (ein mal vorberechneten) Wert 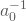 multipliziert, da Multiplikation günstiger ist als Division für viele CPUs.
multipliziert, da Multiplikation günstiger ist als Division für viele CPUs.