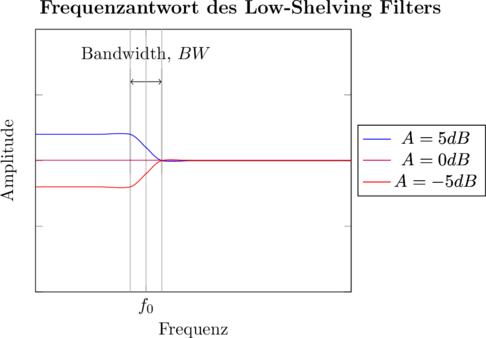
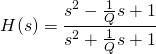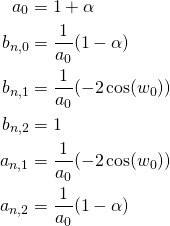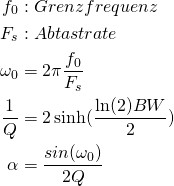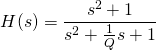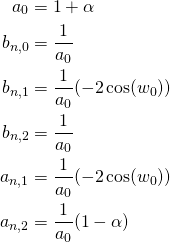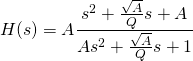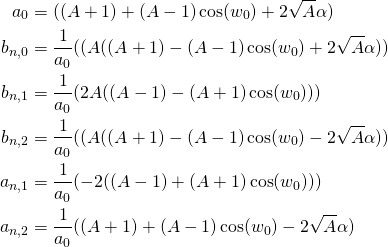Kategorie: Embedded (page 2 of 2)

Digitaler Wah-Wah-Effekt

26. November 2019 / solocan / Noch kein Kommentar

Der Wah-Wah-Effekt ist ein Filtereffekt, der die hohen Frequenzen im Signal herausfiltert (Tiefpass) oder abschwächt (Shelving Filter). Die Filterung wird

mit einem Wahwah-Pedal (Standard-Wahwah Effekt) oder
mit einem LFO (AutoWah)

kontrolliert. Im Fall vom WahWah-Pedal wird die Pedalposition genutzt, um die Frequenz des Tiefpassfilters zu ermitteln. Im Fall vom Auto Wah wird die Frequenz aus dem LFO abgeleitet.

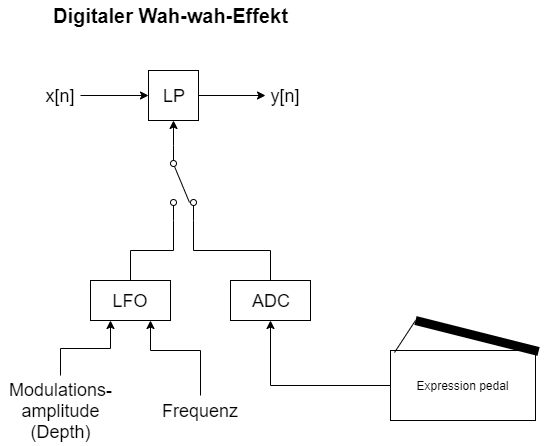
Im folgenden ist das Grundprinzip des Wah-Wah-Effekts aufgezeigt.

Parameter

Folgende Kontrollparameter sind für einen Wah-Wah-Effekt üblich:

Source

Hier wird gewählt, ob die Steuerung mit LFO (Auto Wah) oder mit einem Expression-Pedal erfolgen soll.

Tiefe (Depth)

Mit diesem Parameter kontrolliert man die negative Verstärkung des Filters, im Falle eines Kuhschwanzfilters. (Shelving Filter) Hiermit wählt man, ob man einen milden oder starken Effekt haben möchte.

Breite (Width)

Mit diesem Parameter wählt man die Frequenzschranken der Filterung. Üblicherweise sind diese zwischen 500Hz und 4000Hz. Je breiter der Effekt, desto größer das Intervall.

Implementierung

LFO

LFO steuert das Tiefpassfilter. Nach jeder Änderung werden die Parameter des Tiefpassfilters aktualisiert.

float c_autowah::lfo(void){

	float y_lfo;

	//Calculate LFO value
	y_lfo=sin(a_lfo);

	//Update angle
	a_lfo+=a_step;
	if(a_lfo>=2*PI){
		a_lfo=a_lfo-2*PI;
	}

	return y_lfo;
}

void c_autowah::update_wah_frequency(void){

	float sin_x;

	sin_x=lfo();

	if(i_update>=n_update_reset){
		//Update filter frequency
		frequency=freq_low+(sin_x+1)*freq_scaler;
		wahfilter.set_freq(frequency);
		i_update=0;
	}else{
		i_update++;
	}
}

float c_autowah::lfo(void){

float y_lfo;

//Calculate LFO value

y_lfo=sin(a_lfo);

//Update angle

a_lfo+=a_step;

if(a_lfo>=2*PI){

a_lfo=a_lfo-2*PI;

}

return y_lfo;

}

void c_autowah::update_wah_frequency(void){

float sin_x;

sin_x=lfo();

if(i_update>=n_update_reset){

//Update filter frequency

frequency=freq_low+(sin_x+1)*freq_scaler;

wahfilter.set_freq(frequency);

i_update=0;

}else{

i_update++;

}

Hauptroutine

Der Wah-Wah-Hauptalgorithmus ist dann einfach ein LP-Filter. (In dem Fall als Biquad-Filter implementiert)

/*
Wah wah main routine
*/
float c_autowah::process(float x){

	update_wah_frequency();
	return wahfilter.process(input_gain*x);
}

Wah wah main routine

float c_autowah::process(float x){

update_wah_frequency();

return wahfilter.process(input_gain*x);

}

Klangbeispiele

Anbei ist dieser Algorithmus mit ein paar verschiedenen Parametern zu hören.

Gitarre - Rythmus trocken

Gitarre Rythmus - Autowah Depth 50 - Rate 1.25Hz

Gitarre Rythmus - Autowah Depth 90 - Rate 2.5Hz

Gitarre Rythmus - Autowah Depth 90 - Rate 1.25Hz

Gitarre Rythmus - Autowah Depth 90 - Rate 2.5Hz

Digitaler Tremolo-Effekt

26. November 2019 / solocan / Noch kein Kommentar

Ein Tremolo-Effekt ändert zyklisch die Lautstärke eines Signals. Es wird je nach Parametrierung zum Erzeugen von „Country“-Sounds oder aber auch in starker Ausführung für spezielle Effekte wie „Boulevard of broken dreams“-Intro von Green day.

Im folgenden ist das Grundprinzip des Tremolo-Effekts aufgezeigt.

Parameter

Folgende Kontrollparameter für den Tremolo-Effekt sind üblich:

Frequenz

Mit der Frequenz kontrolliert man die Geschwindigkeit der Verstärkungsmodulation. Üblicherweise in Hertz. Typische Werte zwischen 1Hz und 25Hz.

Tiefe (Depth)

Mit diesem Parameter kontrolliert man die Wirksamkeit der Modulation. Üblicherweise in [%] angegeben. Bei 30% wird die Lautstärke zwischen 70% und 100% gesteuert. Bei 100% wird die Lautstärke zwischen 0 und 100% gesteuert (Also dabei teilweise ganz stummgeschaltet.)

LFO Typ

Damit wird der Typ des LFO-Signals gewählt. Übliche Signale sind:

Sinussignal
Dreiecksignal
Sägezahnsignal
Rechtecksignal

Modulation mit LFO

Während sonstige Tonhöhenmodulationseffekte wie Chorus, Flanger, Rotary mit einem Sinus-Signal kontrolliert wird, sind für den Tremolo-Effekt auch andere Signalquellen üblich. Die effiziente Implementierung dieser Signalgeneratoren sind unten gezeigt.

Implementierung

LFO

/*
LFO
*/
float c_tremolo::lfo(void){

	float y_lfo;

	//Calculate LFO value

	switch(type){
	//Sinus
	case 0:
		y_lfo=0.5*(1+sin(i_lfo));
		//Update angle
		i_lfo+=a_step;
		if(i_lfo>=2*PI){
			i_lfo-=2*PI;
		}
		break;

	//Triangle
	case 1:

		y_lfo = fabs(fmod(i_lfo, 2) -1 );
		i_lfo+=t_step;

		break;
	case 2:		//Square
		y_lfo=fmod(i_lfo,2) < 1 ? 1 : 0;
		i_lfo+=t_step;
		break;

	}

//	printf("%.3f\n",y_lfo);

	return y_lfo;
}

/*
Calculate the gain
*/
float c_tremolo::get_current_attenuation(void){

	return 1-depth*lfo();

}

LFO

float c_tremolo::lfo(void){

float y_lfo;

//Calculate LFO value

switch(type){

//Sinus

case 0:

y_lfo=0.5*(1+sin(i_lfo));

//Update angle

i_lfo+=a_step;

if(i_lfo>=2*PI){

i_lfo-=2*PI;

}

break;

//Triangle

case 1:

y_lfo = fabs(fmod(i_lfo, 2) -1 );

i_lfo+=t_step;

break;

case 2: //Square

y_lfo=fmod(i_lfo,2) < 1 ? 1 : 0;

i_lfo+=t_step;

break;

}

// printf("%.3f\n",y_lfo);

return y_lfo;

}

Calculate the gain

float c_tremolo::get_current_attenuation(void){

return 1-depth*lfo();

}

Hauptroutine

Der Algorithmus vom Rotary-Effekt ist vergleichbar mit einem Chorus-Algorithmus ohne Signalkopie und Trockensignal / Effektsignal-Mischung.

float c_tremolo::process(float x){

	return x*get_current_attenuation();
}

float c_tremolo::process(float x){

return x*get_current_attenuation();

}

Klangbeispiele

Anbei ist dieser Algorithmus mit ein paar verschiedenen Parametern zu hören.

Gitarre - Rythmus trocken

Gitarre - Tremolo Sinus: Depth: 50 - Frequency: 6Hz

Gitarre - Tremolo Dreieck: Depth: 75 - Frequency: 20Hz

Gitarre - Tremolo Rechteck: Depth: 50 - Frequency: 10Hz

Digitaler Rotary-Effekt

26. November 2019 / solocan / Noch kein Kommentar

Ein Rotary-Effekt ist ein Modulationseffekt, der die Frequenz bzw. die Tonhöhe (Pitch) des Eingangssignals mit einem Niedrigfrequenzoszillator (LFO: engl. Low-frequency oscillator) ändert. Somit entsteht eine Rotary bzw. je nach Parametrierung ein Vibrato-artiger Effekt.

Er ist sehr ähnlich zum Chorus-Effekt mit dem Unterschied, dass hierbei das Signal nicht kopiert wird sondern das trockene Signal verarbeitet wird: Ohne Kopieren und zurückmischen. Daher resultiert hierbei kein Phasenauslöschungseffekt.

Im folgenden ist das Grundprinzip des Rotary-Effekts aufgezeigt.

Parameter

Folgende Kontrollparameter sind für einen Flanger-Effekt üblich:

Frequenz

Mit der Frequenz kontrolliert man die Geschwindigkeit der Frequenzmodulation. Üblicherweise in Hertz [Hz]. Typische Werte zwischen 1Hz und 25Hz.

Tiefe (Depth)

Mit diesem Parameter kontrolliert man die Wirksamkeit der Modulation. Sie wird in Prozent oder in Millisekunden (Delay-Zeit) angegeben. Wenn z.B. die Basis-Delayzeit 25ms ist und die Tiefe 50%, dann bedeutet das, dass das Delay zwischen 12,5ms und 37,5ms moduliert wird.

Modulation mit LFO

Ein LFO ist nichts anderes als ein Signalgenerator, der in der Regel ein niederfrequentes Sinus-Signal generiert. Diese Signalquelle nutzt man u. a. zur Modulation eines Signals.

Im Fall eines Rotary-Effekts moduliert man „die Abtastfrequenz“. Konkret tut man das, in dem man die Delay-Zeit kontinuierlich erhöht und reduziert. Diese Delay-Zeit ist in der Regel sehr kurz und liegt im Fall von Chorus in der Regel 5-50ms. Man nimmt eine Referenzdelayzeit. Z.b. 20ms und moduliert diese mit LFO zwischen 10ms und 30ms. Dadurch verlangsamt und beschleunigt das Signal und es entsteht eine Frequenzverschiebung.

Implementierung

LFO

Für das Rotary-Puffer wird ein Kreispuffer benötigt, in dem Eingangssignal aufgenommen wird.

/*
LFO
*/
float c_rotary::lfo(void){

	float y_lfo;

	//Calculate LFO value
	y_lfo=sin(a_lfo);

	//Update angle
	a_lfo+=a_step;
	if(a_lfo>=2*PI){
		a_lfo=a_lfo-2*PI;
	}

	return y_lfo;
}

/*
Calculate rotating delay
*/
float c_rotary::get_current_delay(void){

	//Calculate time
	float t;
	t=d_base+depth*lfo();

	//Return the delay time
	return t;

}

LFO

float c_rotary::lfo(void){

float y_lfo;

//Calculate LFO value

y_lfo=sin(a_lfo);

//Update angle

a_lfo+=a_step;

if(a_lfo>=2*PI){

a_lfo=a_lfo-2*PI;

}

return y_lfo;

}

Calculate rotating delay

float c_rotary::get_current_delay(void){

//Calculate time

float t;

t=d_base+depth*lfo();

//Return the delay time

return t;

}

Hauptroutine

Der Algorithmus vom Rotary-Effekt ist vergleichbar mit einem Chorus-Algorithmus ohne Signalkopie und Trockensignal / Effektsignal-Mischung.

/*
Rotary main routine
*/
float c_rotary::process(float x){

	float y;
	float t_c;	//Current delay

	//Get current delay
	t_c=get_current_delay(); //Delay time

	//Calculate the position of the pointer
	int wptr;

	wptr=rptr-rint(t_c*FSms);

	if(wptr<0){
		wptr+=rotary_len;
	}

	//Calculate output
	y=rbuf[wptr];

	//Update the buffer
	rbuf[rptr]=x;

	//Increment
	rptr++;
	if(rptr>=rotary_len){
		rptr-=rotary_len;
	}

	return y;
}

Rotary main routine

float c_rotary::process(float x){

float y;

float t_c; //Current delay

//Get current delay

t_c=get_current_delay(); //Delay time

//Calculate the position of the pointer

int wptr;

wptr=rptr-rint(t_c*FSms);

if(wptr<0){

wptr+=rotary_len;

}

//Calculate output

y=rbuf[wptr];

//Update the buffer

rbuf[rptr]=x;

//Increment

rptr++;

if(rptr>=rotary_len){

rptr-=rotary_len;

}

return y;

}

Klangbeispiele

Anbei ist dieser Algorithmus mit ein paar verschiedenen Parametern zu hören.

Gitarre - Rythmus trocken

Gitarre Rythmus - Rotary Depth:100 - Freq:2Hz

Gitarre Rythmus - Rotary Depth:100 - Freq:5Hz

Gitarre Rythmus - Rotary Depth:50 - Freq:10Hz

Digitaler Flanger-Effekt

26. November 2019 / solocan / Noch kein Kommentar

Ein Flangereffekt ist ein Modulationseffekt, der das Eingangssignal kopiert und dessen Tonhöhe (Pitch) mit einem Niedrigfrequenzoszillator (LFO: engl. Low-frequency oscillator) ändert. Der Unterschied zum Chorus-Effekt besteht darin, dass auf der Effektlinie eine Rückkopplung gibt. Da die Verzögerung im Bereich von paar Millisekunden liegt, resultieren daraus Phasenlöschungseffekte. Das gibt dem Flanger seinen charakteristischen Space-Sound.

Eine andere Eigenheit vom Flanger ist, dass hierbei üblicherweise auch das trockene Signal verzögert werden muss, um eine starke Phasenauslöschung und einen drehend empfundenen Sound zu erzielen.

Im folgenden ist das Grundprinzip eines Flangers aufgezeigt.

Parameter

Folgende Kontrollparameter sind für einen Flanger-Effekt üblich:

Frequenz

Mit der Frequenz kontrolliert man die Geschwindigkeit der Frequenzmodulation. Üblicherweise in Hertz [Hz]. Typische Werte zwischen 1Hz und 25Hz.

Tiefe (Depth)

Pre-Delay

Die Verzögerung des trockenen Signals. Dies kann parametriert werden, um die Stärke und Charakteristik des Phasenauslöschungseffektes einzustellen.

Wet/Dry

Hiermit wird kontrolliert, wie stark das modulierte Signal ins Ausgangssignal beigemischt werden soll.

Modulation mit LFO

Ein LFO ist nichts anderes als ein Signalgenerator, der in der Regel ein niederfrequentes Sinus-Signal generiert. Diese Signalquelle nutzt man u. a. zur Modulation eines Signals.

Im Fall eines Chorus moduliert man „die Abtastfrequenz“. Konkret tut man das, in dem man die Delay-Zeit kontinuierlich erhöht und reduziert. Diese Delay-Zeit ist in der Regel sehr kurz und liegt im Fall von Chorus in der Regel 5-50ms. Man nimmt eine Referenzdelayzeit. Z.b. 20ms und moduliert diese mit LFO zwischen 10ms und 30ms. Dadurch verlangsamt und beschleunigt das Signal und es entsteht eine Frequenzverschiebung. Dies wird musikalisch als eine Intonation wahrgenommen.

Implementierung

LFO

Für das Flanger-Puffer wird ein Kreispuffer benötigt, in dem Eingangssignal aufgenommen wird.

/*
LFO
*/
float c_flanger::lfo(void){

	float y_lfo;

	//Calculate LFO value
	y_lfo=sin(a_lfo);

	//Update angle
	a_lfo+=a_step;
	if(a_lfo>=2*PI){
		a_lfo=a_lfo-2*PI;
	}

	return y_lfo;
}

/*
Calculate rotating delay
*/
float c_flanger::get_current_delay(void){

	//Calculate time
	float t;
	t=(float)d_base+depth*lfo();

	//Return the delay time
	return t;

}

LFO

float c_flanger::lfo(void){

float y_lfo;

//Calculate LFO value

y_lfo=sin(a_lfo);

//Update angle

a_lfo+=a_step;

if(a_lfo>=2*PI){

a_lfo=a_lfo-2*PI;

}

return y_lfo;

}

Calculate rotating delay

float c_flanger::get_current_delay(void){

//Calculate time

float t;

t=(float)d_base+depth*lfo();

//Return the delay time

return t;

}

Hauptroutine

Der Algorithmus vom Chorus ist vergleichbar mit einem Delay-Algorithmus ohne Feedback und mit variabler Delay-Zeit.

/* 
Flanger main process
*/
float c_flanger::process(float x){

	float y;

	float t_c;	//Current delay

	//Get tap distance
	t_c=get_current_delay(); //Tap distance

	//Calculate the position of the pointer
	int wptr;

	wptr=fptr-lrint(t_c*FSms);

	if(wptr<0){
		wptr+=flanger_len;
	}

	//Calculate output
	y=G_d*drybuf[dryptr] + G_w*fbuf[wptr];

	//Update the buffer
	fbuf[fptr]=x+G_fb*fbuf[wptr];
	drybuf[dryptr]=x;

	//Increment
	fptr++;
	if(fptr>=flanger_len){
		fptr=0;
	}

	dryptr++;
	if(dryptr>=l_drybuf){
		dryptr=0;
	}

	return y;
}

Flanger main process

float c_flanger::process(float x){

float y;

float t_c; //Current delay

//Get tap distance

t_c=get_current_delay(); //Tap distance

//Calculate the position of the pointer

int wptr;

wptr=fptr-lrint(t_c*FSms);

if(wptr<0){

wptr+=flanger_len;

}

//Calculate output

y=G_d*drybuf[dryptr] + G_w*fbuf[wptr];

//Update the buffer

fbuf[fptr]=x+G_fb*fbuf[wptr];

drybuf[dryptr]=x;

//Increment

fptr++;

if(fptr>=flanger_len){

fptr=0;

}

dryptr++;

if(dryptr>=l_drybuf){

dryptr=0;

}

return y;

}

Ein Prozess ohne Verzögerung vom trockenen Signal sieht folgendermaßen aus:

/*
Main process without delay on dry line
*/
float c_flanger::process_nondelay(float x){

	float y;

	float t_c;	//Current delay

	//Get tap distance
	t_c=get_current_delay(); //Tap distance

	//Calculate the position of the pointer
	int wptr;

	wptr=fptr-lrint(t_c*FSms);

	if(wptr<0){
		wptr+=flanger_len;
	}

	//Calculate output
	y=G_d*x + G_w*fbuf[wptr];

	//Update the buffer
	fbuf[fptr]=x+G_fb*fbuf[wptr];

	//Increment
	fptr++;
	if(fptr>=flanger_len){
		fptr=0;
	}

	return y;
}

Main process without delay on dry line

float c_flanger::process_nondelay(float x){

float y;

float t_c; //Current delay

//Get tap distance

t_c=get_current_delay(); //Tap distance

//Calculate the position of the pointer

int wptr;

wptr=fptr-lrint(t_c*FSms);

if(wptr<0){

wptr+=flanger_len;

}

//Calculate output

y=G_d*x + G_w*fbuf[wptr];

//Update the buffer

fbuf[fptr]=x+G_fb*fbuf[wptr];

//Increment

fptr++;

if(fptr>=flanger_len){

fptr=0;

}

return y;

}

Klangbeispiele

Anbei ist dieser Algorithmus mit ein paar verschiedenen Parametern zu hören.

Gitarre - Rythmus trocken

Gitarre Rythmus - Flanger - Depth:50 - Rate: 1 - FB:50

Gitarre Rythmus - Flanger - Depth:50 - Rate: 2 - FB:20

Gitarre Rythmus - Flanger - Depth:50 - Rate: 2 - FB:50

Gitarre Rythmus - Flanger - Depth:10 - Rate: 2 - FB:50

Gitarre Rythmus - Flanger - Depth:10 - Rate: 10 - FB:70

Digitaler Chorus-Effekt

26. November 2019 / solocan / Noch kein Kommentar

Ein Choruseffekt (engl. für Chor-Effekt) ist ein Modulationseffekt, der das Eingangssignal kopiert und dessen Tonhöhe (Pitch) mit einem Niedrigfrequenzoszillator (LFO: engl. Low-frequency oscillator) ändert. Somit entsteht eine „imperfekte“ Kopie vom Eingangssignal, das dem Ausgangssignal beigemischt wird. Dadurch entsteht der sogenannte Chor-Effekt. Im folgenden ist das Grundprinzip eines Chorus aufgezeigt.

Im obigen Diagramm gibt es nur eine Kopie des Eingangssignals (single-tap). Es ist auch üblich mehrere Kopien zu machen und mit verschiedenen Parametern einen „mehrköpfigen“ Chor zu erzielen.

Parameter

Folgende Kontrollparameter sind für einen Chorus-Effekt üblich:

Frequenz

Mit der Frequenz kontrolliert man die Geschwindigkeit der Frequenzmodulation. Üblicherweise in Hertz [Hz]. Typische Werte zwischen 1Hz und 25Hz.

Tiefe (Depth)

Wet/Dry

Hiermit wird kontrolliert, wie stark das modulierte Signal ins Ausgangssignal beigemischt werden soll.

Multi-Tap

Man kann das Eingangssignal auch mehr als ein mal abzweigen und modulieren. Wenn man die Einstellungen nicht für jeden Tap vornehmen will, kann man diese algorithmisch beliebig zusammensetzen.

Modulation mit LFO

Ein LFO ist nichts anderes als ein Signalgenerator, der in der Regel ein niederfrequentes Sinus-Signal generiert. Diese Signalquelle nutzt man u. a. zur Modulation eines Signals.

Implementierung

LFO

Für das Chorus-Puffer wird ein Kreispuffer benötigt, in dem Eingangssignal aufgenommen wird. Beim Multi-tap-Chorus braucht man nicht mehrere Puffer sondern nur mehrere LFOs und mehrere Zeiger auf das Puffer.

/*
LFO
*/
float c_chorus::lfo(void){

	float y_lfo;

	//Calculate LFO value
	y_lfo=sin(a_lfo);

	//Update angle
	a_lfo+=a_step;
	if(a_lfo>=2*PI){
		a_lfo=a_lfo-2*PI;
	}

	return y_lfo;
}

/*
Calculate rotating delay
*/
float c_chorus::get_current_delay(void){

	//Calculate time
	float t;
	t=d_base+depth*lfo();

	//Return the delay time
	return t;

}

LFO

float c_chorus::lfo(void){

float y_lfo;

//Calculate LFO value

y_lfo=sin(a_lfo);

//Update angle

a_lfo+=a_step;

if(a_lfo>=2*PI){

a_lfo=a_lfo-2*PI;

}

return y_lfo;

}

Calculate rotating delay

float c_chorus::get_current_delay(void){

//Calculate time

float t;

t=d_base+depth*lfo();

//Return the delay time

return t;

}

Hauptroutine

Der Algorithmus vom Chorus ist vergleichbar mit einem Delay-Algorithmus ohne Feedback und mit variabler Delay-Zeit.

/*
Main chorus single tap
*/
float c_chorus::process(float x){

	float y;

	float t_c;	//Current delay

	//Get tap distance
	t_c=get_current_delay(); //Tap distance

	//Calculate the position of the pointer
	int wptr;

	wptr=cptr-lrint(t_c*FSms);

	if(wptr<0){
		wptr+=chorus_len;
	}

	//Calculate output
	y=G_d*x + G_w*cbuf[wptr];

	//Update the buffer
	cbuf[cptr]=x;

	//Increment
	cptr++;
	if(cptr>=chorus_len){
		cptr-=chorus_len;
	}

	return y;
}

Main chorus single tap

float c_chorus::process(float x){

float y;

float t_c; //Current delay

//Get tap distance

t_c=get_current_delay(); //Tap distance

//Calculate the position of the pointer

int wptr;

wptr=cptr-lrint(t_c*FSms);

if(wptr<0){

wptr+=chorus_len;

}

//Calculate output

y=G_d*x + G_w*cbuf[wptr];

//Update the buffer

cbuf[cptr]=x;

//Increment

cptr++;

if(cptr>=chorus_len){

cptr-=chorus_len;

}

return y;

}

Klangbeispiele

Anbei ist dieser Algorithmus mit ein paar verschiedenen Parametern zu hören.

Gitarre - Rythmus trocken

Gitarre - Rythmus Chorus - Depth: 10 - Rate: 7Hz

Gitarre - Rythmus Chorus - Depth: 50 - Rate: 7Hz

Gitarre - Rythmus Chorus - Depth: 90 - Rate: 7Hz

Gitarre - Rythmus Chorus - Depth: 50 - Rate: 2Hz

Gitarre - Rythmus Chorus - Depth: 50 - Rate: 15Hz

Digitales Delay

22. November 2019 / solocan / Noch kein Kommentar

Ein Delay (Engl. für Verzögerung) ist in digitaler Ausführung -im Gegensatz zu analog- ein recht simpel zu implementierender Effekt. In der Grundform ohne Rückkopplung verzögert es das Eingangssignal um einen voreingestellten Zeitversatz und mischt das verzögerte Signal zum Eingangssignal (trockenes Signal) bei. Dabei entsteht ein Delay-Effekt. Mit der Rückkopplung, siehe Abbildung, wird das verzögerte Signal durch ein Feedbackverstärkung $G_{FB}$ abgeschwächt und zum Eingangssignal der Verzögerungseingang $a[n]$ zurückgemischt.

Parameter

Folgende Kontrollparameter sind für einen Flanger-Effekt üblich:

Delay-Zeit

Einstellung der Delay-Zeit. Üblicherweise in Millisekunden. Oft wird zur Angabe der Delay-Zeit eine „Tapping“ Funktion zur Verfügung gestellt, mit der der Benutzer den Takt mit einem Taster vorgeben kann und dieser Takt wird in die Zeit umgerechnet.

Takt

Der Parameter, ob der angetippter Takt als z.B. als Viertel, Achtel oder Sechszehntel zu verstehen ist.

Rückkopplungsdämpfung (Feedback gain)

Mit diesem Parameter kontrolliert man die Dämpfung der Rückkopplung. Aus Stabilitsgründen muss sich diese im Intervall von

(1) $\begin{equation*} 0 \leq G_{FB} <1 \end{equation*}$

befinden.

Multi-Tap

Man kann das Eingangssignal auch mehr als ein mal abzweigen und verzögern. Wenn man die Einstellungen nicht für jeden Tap vornehmen will, kann man diese algorithmisch beliebig zusammensetzen (lassen).

Pre-Delay

Die Verzögerung des trockenen Signals.

Wet/Dry

Hiermit wird kontrolliert, wie stark das verzögerte Signal ins Ausgangssignal beigemischt werden soll.

Implementierung

Für das Delay wird ein großes Kreispuffer für $z^{-M}= benötigt, in dem Delay-Signal aufgenommen wird.

/*Main process of delay line */
float c_delay::process(float x){

	float y;

	//Calculate output
	y=dbuf[dptr]*G_w+x*G_d;

	//Update buffer
	dbuf[dptr]=x+dbuf[dptr]*G_fb;

	//Increment pointer (circular buffer)
	dptr++;

        //Reset pointer (circular buffer)
	if(dptr>=n_distance){
		dptr=0;
	}

	return y;
}

/*Main process of delay line */

float c_delay::process(float x){

float y;

//Calculate output

y=dbuf[dptr]*G_w+x*G_d;

//Update buffer

dbuf[dptr]=x+dbuf[dptr]*G_fb;

//Increment pointer (circular buffer)

dptr++;

//Reset pointer (circular buffer)

if(dptr>=n_distance){

dptr=0;

}

return y;

}

Die Variable n_distance ist das Delay time umgerechnet in Anzahl der Samples und berechnet sich (nach jedem Delay-Time update) folgendermaßen:

/*
Routine for setting the delay time
*/
void c_delay::set_time(float *time){

        //Delay time is incoming as milliseconds
	delay_time=*time
	n_distance=(unsigned long)(*time*FSms);

	//Security for delay length
	if(n_distance>delay_max){
		n_distance=delay_max;
	}

	reset_buffer();

}

Routine for setting the delay time

void c_delay::set_time(float *time){

//Delay time is incoming as milliseconds

delay_time=*time

n_distance=(unsigned long)(*time*FSms);

//Security for delay length

if(n_distance>delay_max){

n_distance=delay_max;

}

reset_buffer();

}

Klangbeispiele

Anbei ist dieser Algorithmus mit ein paar verschiedenen Parametern zu hören.

Gitarre - Rythmus trocken

Gitarre - Rythmus Delay-Time: 600ms - Feedback: 0.5 - Wet gain:0.2

Gitarre - Rythmus Delay-Time: 300ms - Feedback: 0 - Wet gain:0.2

Gitarre - Rythmus Delay-Time: 300ms - Feedback: 0.5 - Wet gain:0.2

Gitarre - Rythmus Delay-Time: 300ms - Feedback: 0.9 - Wet gain:0.2

Digitales Allpassfilter

21. November 2019 / solocan / Noch kein Kommentar

Das Allpassfilter lässt alle Frequenzen durch, verursacht allerdings eine Phasenverschiebung, welches als Verzögerungselement verwendet werden kann.

Die Übertragungsfunktion eines digitalen Allpassfilters 2. Ordnung kann als

(1) $\begin{equation*} H(s)=\frac{s^2-\frac{1}{Q}s+1}{s^2+\frac{1}{Q}s+1} \end{equation*}$

beschrieben werden.

Ermittlung der Koeffizienten für das Biquad-filter

Nach der bilinearen Transformation erhält man

(2) $\begin{equation*} \begin{align} a_0&=1+\alpha \\ b_{n,0}&=\frac{1}{a_0} (1-\alpha) \\ b_{n,1}&=\frac{1}{a_0} (-2 \cos(w_0))\\ b_{n,2}&=1\\ a_{n,1}&=\frac{1}{a_0} (-2 \cos(w_0))\\ a_{n,2}&=\frac{1}{a_0} (1-\alpha) \\ \end{align} \end{equation*}$

wobei

(3) $\begin{equation*} \begin{align} f_0 &: Grenzfrequenz\\ F_s&: Abtastrate\\ \omega_0&=2 \pi \frac{f_0}{F_s}\\ \frac{1}{Q}&=2 \sinh(\frac{\ln(2) BW}{2})\\ \alpha&=\frac{sin(\omega_0)}{2 Q} \end{align} \end{equation*}$

Implementierung

Somit erhält man alle Koeffizienten, die man für die Implementierung braucht. Die Implementierung der Koeffizientenberechnung würde folgendermaßen aussehen.

//Deklaration
double A,w0,cosw0,sinw0,alpha,a0;

//Hilfsvariablen
A=pow(10,gain/40);
w0=2*PI*(f0/FS);
cosw0=cos(w0);
sinw0=sin(w0);
alpha=sinw0/(2*Q);

//Normalisierungsparameter
a0_inv=1/(1+alpha);

//Koeffizientenberechnung
bn0=a0_inv;
bn1=(float)((-2 cosw0)*a0_inv);
bn2=1;
an1=(float)((-2 cosw0)*a0_inv);
an2=(float)((1-alpha)*a0_inv);

//Deklaration

double A,w0,cosw0,sinw0,alpha,a0;

//Hilfsvariablen

A=pow(10,gain/40);

w0=2*PI*(f0/FS);

cosw0=cos(w0);

sinw0=sin(w0);

alpha=sinw0/(2*Q);

//Normalisierungsparameter

a0_inv=1/(1+alpha);

//Koeffizientenberechnung

bn0=a0_inv;

bn1=(float)((-2 cosw0)*a0_inv);

bn2=1;

an1=(float)((-2 cosw0)*a0_inv);

an2=(float)((1-alpha)*a0_inv);

Am Code lassen sich manche Optimierungen erkennen.

Mehrmals vorkommende Variablen sind vorberechnet (z.B. trigonometrische Funktionen)
Anstatt jedes mal durch $a_0$ zu teilen, wird mit inversem (ein mal vorberechneten) Wert $a_0^{-1}$ multipliziert, da Multiplikation günstiger ist als Division für viele CPUs.
Die Berechnungen erfolgen mit Gleitkommezahlen doppelter Präzision (double) und wird am Ende auf Float gecastet. Der Grund: Trigonometrischen Funktionen mit Single-Präzision (float) kann zu erheblichen numerischen Fehlern und dadurch zu unerwünschten Ergebnissen bzw. Instabilität führen.
Der Code ist optimiert für die Hardware-FPU von Cortex-M7 Mikroprozessor.

Digitales Kerbfilter (Notch filter)

21. November 2019 / solocan / Noch kein Kommentar

Das Kerbfilter (engl. Notch filter) sperrt eine Frequenz bzw. einen sehr engen Frequenzbereich um $f_0$ , während es den Rest des Spektrums durchlässt.

Rendered by QuickLaTeX.com

Die Übertragungsfunktion eines digitalen Kerbfilters 2. Ordnung kann als

(1) $\begin{equation*} H(s)=\frac{s^2+1}{s^2+\frac{1}{Q}s+1} \end{equation*}$

beschrieben werden.

Ermittlung der Koeffizienten für das Biquad-filter

Nach der bilinearen Transformation erhält man

(2) $\begin{equation*} \begin{align} a_0&=1+\alpha \\ b_{n,0}&=\frac{1}{a_0} \\ b_{n,1}&=\frac{1}{a_0} (-2 \cos(w_0))\\ b_{n,2}&=\frac{1}{a_0} \\ a_{n,1}&=\frac{1}{a_0} (-2 \cos(w_0))\\ a_{n,2}&=\frac{1}{a_0} (1-\alpha) \\ \end{align} \end{equation*}$

wobei

Implementierung

Somit erhält man alle Koeffizienten, die man für die Implementierung braucht. Die Implementierung der Koeffizientenberechnung würde folgendermaßen aussehen.

//Deklaration
double A,w0,cosw0,sinw0,alpha,a0;

//Hilfsvariablen
A=pow(10,gain/40);
w0=2*PI*(f0/FS);
cosw0=cos(w0);
sinw0=sin(w0);
alpha=sinw0/(2*Q);

//Normalisierungsparameter
a0_inv=1/(1+alpha);

//Koeffizientenberechnung
bn0=a0_inv;
bn1=(float)((-2 cosw0)*a0_inv);
bn2=a0_inv;
an1=(float)((-2 cosw0)*a0_inv);
an2=(float)((1-alpha)*a0_inv);

//Deklaration

double A,w0,cosw0,sinw0,alpha,a0;

//Hilfsvariablen

A=pow(10,gain/40);

w0=2*PI*(f0/FS);

cosw0=cos(w0);

sinw0=sin(w0);

alpha=sinw0/(2*Q);

//Normalisierungsparameter

a0_inv=1/(1+alpha);

//Koeffizientenberechnung

bn0=a0_inv;

bn1=(float)((-2 cosw0)*a0_inv);

bn2=a0_inv;

an1=(float)((-2 cosw0)*a0_inv);

an2=(float)((1-alpha)*a0_inv);

Am Code lassen sich manche Optimierungen erkennen.

Mehrmals vorkommende Variablen sind vorberechnet (z.B. trigonometrische Funktionen)
Anstatt jedes mal durch $a_0$ zu teilen, wird mit inversem (ein mal vorberechneten) Wert $a_0^{-1}$ multipliziert, da Multiplikation günstiger ist als Division für viele CPUs.
Die Berechnungen erfolgen mit Gleitkommezahlen doppelter Präzision (double) und wird am Ende auf Float gecastet. Der Grund: Trigonometrischen Funktionen mit Single-Präzision (float) kann zu erheblichen numerischen Fehlern und dadurch zu unerwünschten Ergebnissen bzw. Instabilität führen.
Der Code ist optimiert für die Hardware-FPU von Cortex-M7 Mikroprozessor.

Kuhschwanzfilter 2 – Low shelving filter

21. November 2019 / solocan / Noch kein Kommentar

Das Kuhschwanzfilter für Tiefenanpassung (engl. Low shelving filter) verstärkt oder dämpft einen Frequenzbereich unter $f_0$ gleichmäßig, während es die die höheren Frequenzen des Spektrums unverändert durchlässt.

Rendered by QuickLaTeX.com

Die Übertragungsfunktion eines digitalen Low-Shelving Filters 2. Ordnung kann als

(1) $\begin{equation*} H(s)=A \frac{s^2+\frac{\sqrt{A}}{Q}s+A}{As^2+\frac{\sqrt{A}}{Q}s+1} \end{equation*}$

beschrieben werden.

Ermittlung der Koeffizienten für das Biquad-filter

Nach der bilinearen Transformation erhält man

(2) $\begin{equation*} \begin{align} a_0&=((A+1)+(A-1) \cos(w_0)+2 \sqrt{A} \alpha) \\ b_{n,0}&=\frac{1}{a_0}((A ((A+1)-(A-1) \cos(w_0)+2 \sqrt{A} \alpha)) \\ b_{n,1}&=\frac{1}{a_0}(2 A ((A-1)-(A+1) \cos(w_0)))\\ b_{n,2}&=\frac{1}{a_0}((A ((A+1)-(A-1) \cos(w_0)-2 \sqrt{A} \alpha)) \\ a_{n,1}&=\frac{1}{a_0} (-2 ((A-1)+(A+1) \cos(w_0)))\\ a_{n,2}&=\frac{1}{a_0} ((A+1)+(A-1) \cos(w_0)-2 \sqrt{A} \alpha) \\ \end{align} \end{equation*}$

wobei

Implementierung

Somit erhält man alle Koeffizienten, die man für die Implementierung braucht. Die Implementierung der Koeffizientenberechnung würde folgendermaßen aussehen.

//Deklaration
double A,w0,cosw0,sinw0,alpha,a0;

//Hilfsvariablen
A=pow(10,gain/40);
w0=2*PI*(f0/FS);
cosw0=cos(w0);
sinw0=sin(w0);
alpha=sinw0/(2*Q);

//Normalisierungsparameter
a0_inv=1/((A+1)+(A-1)*cosw0+2*sqrt(A)*alpha);

//Koeffizientenberechnung
bn0=(float)((A*((A+1)-(A-1)*cosw0+2*sqrt(A)*alpha))*a0_inv);
bn1=(float)((2*A*((A-1)-(A+1)*cosw0))*a0_inv);
bn2=(float)((A*((A+1)-(A-1)*cosw0-2*sqrt(A)*alpha))*a0_inv);
an1= (float)((-2*((A-1)+(A+1)*cosw0))*a0_inv);
an2=(float)(((A+1)+(A-1)*cosw0-2*sqrt(A)*alpha)*a0_inv);

//Deklaration

double A,w0,cosw0,sinw0,alpha,a0;

//Hilfsvariablen

A=pow(10,gain/40);

w0=2*PI*(f0/FS);

cosw0=cos(w0);

sinw0=sin(w0);

alpha=sinw0/(2*Q);

//Normalisierungsparameter

a0_inv=1/((A+1)+(A-1)*cosw0+2*sqrt(A)*alpha);

//Koeffizientenberechnung

bn0=(float)((A*((A+1)-(A-1)*cosw0+2*sqrt(A)*alpha))*a0_inv);

bn1=(float)((2*A*((A-1)-(A+1)*cosw0))*a0_inv);

bn2=(float)((A*((A+1)-(A-1)*cosw0-2*sqrt(A)*alpha))*a0_inv);

an1= (float)((-2*((A-1)+(A+1)*cosw0))*a0_inv);

an2=(float)(((A+1)+(A-1)*cosw0-2*sqrt(A)*alpha)*a0_inv);

Am Code lassen sich manche Optimierungen erkennen.

Mehrmals vorkommende Variablen sind vorberechnet (z.B. trigonometrische Funktionen)
Anstatt jedes mal durch $a_0$ zu teilen, wird mit inversem (ein mal vorberechneten) Wert $a_0^{-1}$ multipliziert, da Multiplikation günstiger ist als Division für viele CPUs.
Die Berechnungen erfolgen mit Gleitkommezahlen doppelter Präzision (double) und wird am Ende auf Float gecastet. Der Grund: Trigonometrischen Funktionen mit Single-Präzision (float) kann zu erheblichen numerischen Fehlern und dadurch zu unerwünschten Ergebnissen bzw. Instabilität führen.
Der Code ist optimiert für die Hardware-FPU von Cortex-M7 Mikroprozessor.

Klangbeispiele

Gitarre - Rythmus trocken

Gitarre - Rythmus Low shelf 10db 400Hz

Gitarre - Rythmus Low shelf -10db 400Hz

Embedded

17. November 2019 / solocan / Noch kein Kommentar

Übersicht Embedded