Wenn die Filterfunktionen im zeitkontinuierlichen Raum vorliegen, müssen diese zur Implementierung als digitales Filter in den zeitdiskreten Raum transformiert werden. Der Grund dafür ist, dass wir bei der digitalen Signalverarbeitung zeitlich abgetastete Signale haben. Das erfolgt durch die Ersetzung der Punkte ![]() in der S-Ebene:
in der S-Ebene:
(1) 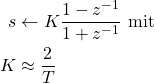
wobei ![]() das zeitliche Abtastintervall, also der Kehrwert von der Abtastrate ist:
das zeitliche Abtastintervall, also der Kehrwert von der Abtastrate ist: ![]() .
.
Zur Frequenzentzerrung muss wird ![]() folgendermaßen ersetzt:
folgendermaßen ersetzt:
(2) ![]()
Somit können die Variablen der zeitkontinuerlichen Achse ![]() ersetzt werden, um die Gleichung in den z-Bereich zu transformieren.
ersetzt werden, um die Gleichung in den z-Bereich zu transformieren.
Diese führt jedoch zu sehr komplexen Gleichungen, wonach die analytische Berechnung der Koeffizienten ohne Softwarehilfe sehr schwierig wird. Daher müssen manche Vereinfachungen vorgenommen werden. Dazu wurden die ![]() –Ersatzgleichungen von Robert Bristow-Johnson aus seinem Audio-Kochbuch genommen.
–Ersatzgleichungen von Robert Bristow-Johnson aus seinem Audio-Kochbuch genommen.
Vereinfachung der Entzerrung nach Robert Bristow-Johnson
Hierfür wurde zur Entzerrung folgender Ersatz genommen.
(3) ![]()
mit
(4) 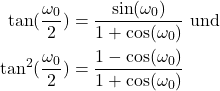
ergeben sich die Ersatzgleichungen
(5) 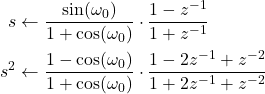
Wenn man nun einen weiteren Vereinfachungsschritt vornimmt und alle Gleichungen mit
(6) ![]()
multipliziert, erhält man
(7) 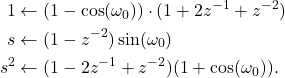
Nun können die ![]() in der zeitkontinuerlichen Übertragungsfunktion ersetzt und die zeitdiskrete Differentialgleichungen berechnet werden.
in der zeitkontinuerlichen Übertragungsfunktion ersetzt und die zeitdiskrete Differentialgleichungen berechnet werden.

1. Januar 2020 — 23:34
this looks pretty good. i wouldn’t have other suggestions for you at this time.
keep in mind that the Bilinear Transform is not the only mapping of z to s. there is Euler’s forward method and Euler’s backward method and other methods for discretizing differential equations.