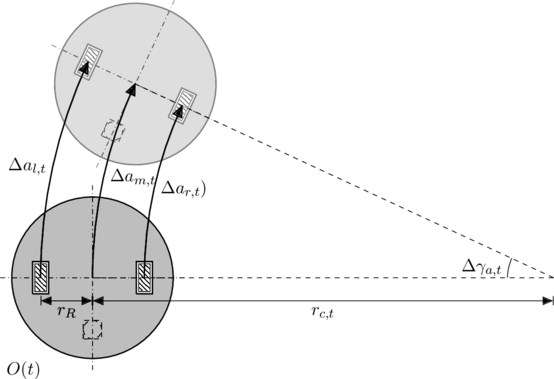
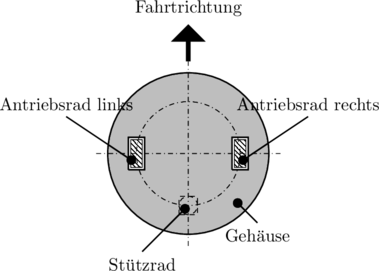
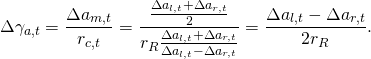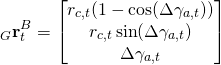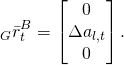Roboter Raspberry Pi, (Ropi) ist ein mobiler Indoor-Roboter, der für den Einsatz auf planaren Flächen ausgelegt ist. Seine Bauform ist in der Abbildung 1 beschrieben.
Beschreibung der Kinematik
Der Ropi wird mit zwei rollenden, unabhängigen Rädern angetrieben und einem dritten, frei drehenden Stützrad abgestützt. Um eine Drehung um eigene Achse zu ermöglichen, befinden sich alle Räder tangential in einem Kreis. Damit sich der Roboter an jeder Stelle um sich drehen kann, ist sein Gehäuse kreisförmig konstruiert, siehe Abbildung 1.
Im Folgenden möchte ich die Kinematik des Roboters beschreiben. Erst betrachte man die freien Körper unter Vernachlässigung der kontinuummechanischen Phänomene wie Deformation als Starrkörper. Die einzelnen freien Körper eines Mehrkörpersystems haben jeweils ![]() Freiheitsgrade, die mit kartesischen Raumkoordinaten beschrieben werden können. D.h. die Lagevektoren der einzelnen freien Körper lassen sich als
Freiheitsgrade, die mit kartesischen Raumkoordinaten beschrieben werden können. D.h. die Lagevektoren der einzelnen freien Körper lassen sich als
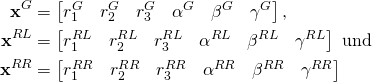
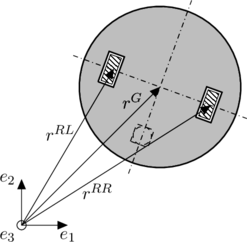
formulieren, wobei die Hochindexen ![]() für Gehäuse,
für Gehäuse, ![]() für das rechte Rad,
für das rechte Rad, ![]() für das linke Rad; die
für das linke Rad; die ![]() die Komponenten des translatorischen Lagevektors in den orthogonalen raumfesten Einheitsvektoren
die Komponenten des translatorischen Lagevektors in den orthogonalen raumfesten Einheitsvektoren ![]() und die
und die ![]() ,
, ![]() ,
, ![]() die Drehungen um die
die Drehungen um die ![]() sind, siehe Abbildung 2.
sind, siehe Abbildung 2.
Nun können wir die Zwangsbedingungen stellen, die die Bindungen des Systems beschreiben. Bei den Zwangsbedingungen unterscheidet man zwischen den holonomen und nichtholonomen Zwangsbedingungen. Die holonomen Zwangsbedingungen beschränken die Lagegrößen und dadurch direkt Geschwindigkeits- und Beschleunigungsgrößen. Die nichtholonomen Zwangsbedingungen hingegen beschränken primär die Geschwindigkeitsgrößen. Die ![]() Matrix der holonomen Zwangsbedingungen lassen sich in impliziter Form als
Matrix der holonomen Zwangsbedingungen lassen sich in impliziter Form als
(1) 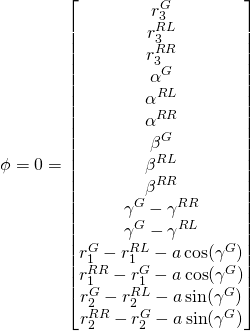
formulieren, wobei ![]() der Radius des Kreises ist, auf dessen Tangente sich die Räder bewegen. Die Freiheitsgrade der Lagegrößen berechnet sich bei Mehrkörpersystemen durch
der Radius des Kreises ist, auf dessen Tangente sich die Räder bewegen. Die Freiheitsgrade der Lagegrößen berechnet sich bei Mehrkörpersystemen durch
(2) ![]()
mit ![]() Körpern und
Körpern und ![]() Zwangsbedingungen. Somit ergeben sich
Zwangsbedingungen. Somit ergeben sich ![]() Freiheitsgrade der Lagegrößen. Der Vektor der Lagegrößen ergibt sich als
Freiheitsgrade der Lagegrößen. Der Vektor der Lagegrößen ergibt sich als
(3) 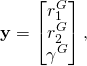
d.H. die Lage des Roboters in der Ebene lässt sich mit zwei translatorischen Größen in der Ebene ![]() und eine Drehung um die
und eine Drehung um die ![]() eines raumfesten Koordinatensystems beschreiben.
eines raumfesten Koordinatensystems beschreiben.
Zusätzlich zu den holonomen Bindungen und hat das Mehrkörpersystem eine nichtholonome Bindung bzw. Zwangsbedingung, die aus der Rollbedingung der Räder hervorgeht. Die Lage des Roboters kann man zwar stets mit dem Lagevektor ![]() beschreiben, allerdings der Roboter kann nicht zu allen möglichen Lagen direkt gesteuert werden. Sondern er muss gegebenenfalls einen indirekten und unbeliebigen Pfad zur erwünschten Lage folgen. Der
beschreiben, allerdings der Roboter kann nicht zu allen möglichen Lagen direkt gesteuert werden. Sondern er muss gegebenenfalls einen indirekten und unbeliebigen Pfad zur erwünschten Lage folgen. Der ![]() Vektor der nichtholonomen Zwangsbedingungen lässt sich in impliziter Form als
Vektor der nichtholonomen Zwangsbedingungen lässt sich in impliziter Form als
(4) ![]()
beschreiben. Das bedeutet, die resultierende \glqq Quergeschwindigkeit\grqq\ muss stets ![]() betragen. Somit erhält man eine zusätzliche Reduktion beim Vektor der Geschwindigkeit, siehe EberhardSchiehlen04.
betragen. Somit erhält man eine zusätzliche Reduktion beim Vektor der Geschwindigkeit, siehe EberhardSchiehlen04.
Der Vektor der Geschwindigkeit lautet demnach
(5) ![]()
mit der Vorwärtsgeschwindigkeit
(6) ![]()
Bisher wird die Kinematik des Roboters im Bezug eines raumfesten kartesischen Koordinatensystems beschrieben. Um die Bewegungen des Roboters zu beschreiben, bietet es sich an, mindestens ein zusätzliches körperfestes und bewegtes Koordinatensystem zu benutzen, z.B. als Sollpfad bei der Regelungsaufgabe. Als Sonderfall für Starrkörpersysteme lässt sich die Bewegung des Mehrkörpersystems vollständig mit bewegten Koordinatensystem beschreiben, wenn die kontinuumsmechanischen Phänomene vernachlässigt werden. Da der Roboter zunächst als ein starres Mehrkörpersystem betrachtet wird, kann dies gewagt werden. Auf die Formulierung der bewegten Koordinatensysteme wird im nächsten Teil eingegangen.
Die Theorie und die Notation basieren in diesem Text größtenteils auf den Skripten und Büchern des Prof. Peter Eberhard und Prof. Werner Schiehlen