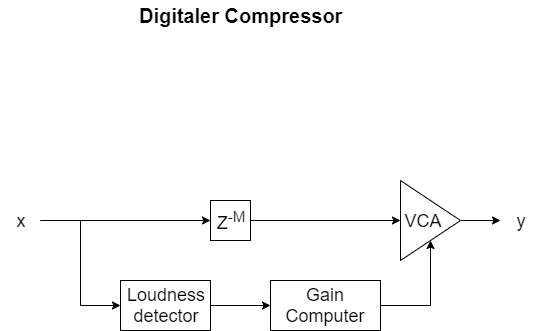
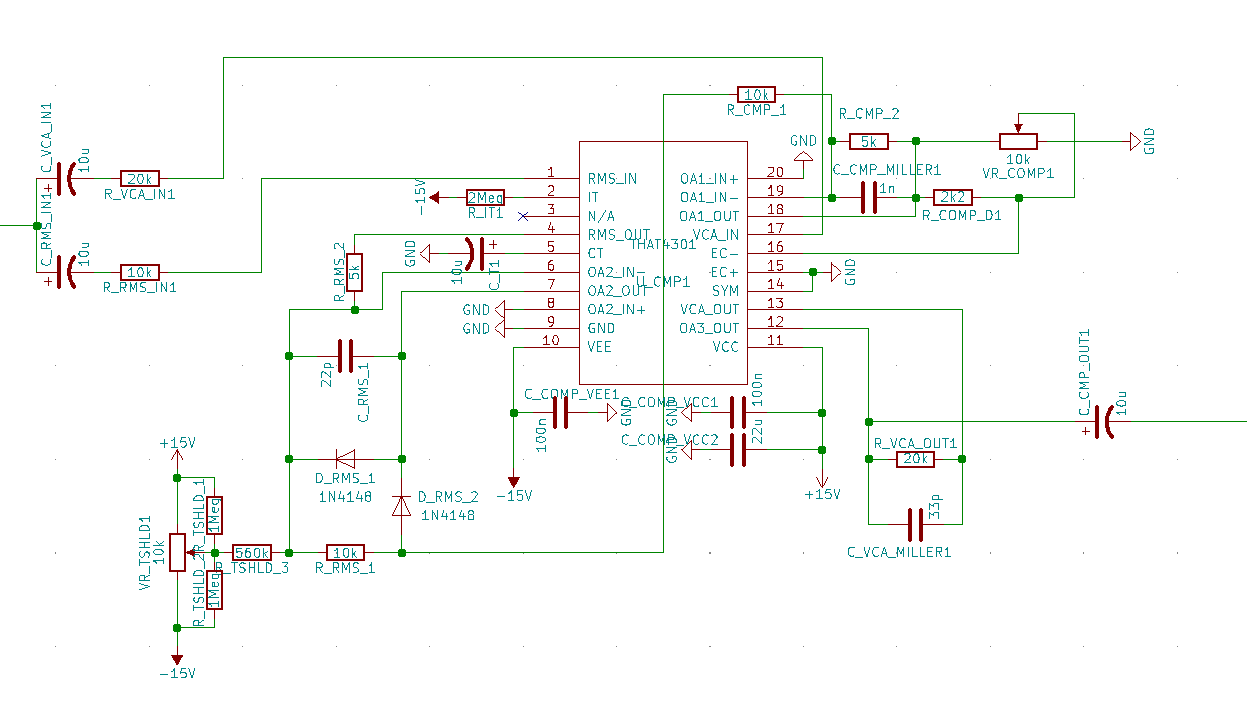
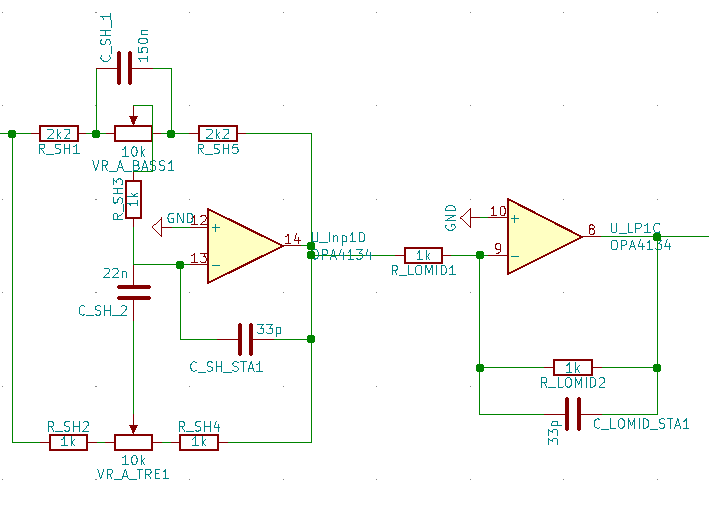
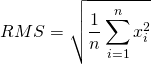Author: solocan (page 2 of 8)

Eine effiziente Methode zur Frequenzerkennung

12. Dezember 2019 / solocan / Noch kein Kommentar

Die Frequenzerkennung (engl. Pitch detection, frequency detection) ist ein Prozess, mit dem man die dominantesten Frequenzen eines Audio-Abschnitts berechnet. Hierbei muss betont werden, dass ein Audio-Abschnitt nicht eine einzige Schwingung mit einer Frequenz besitzt. Er ist vielmehr eine Zusammensetzung von vielen Grundschwingungen, die sich zu jedem Zeitpunkt ändert. Wir nehmen z.B. die Gitarre: Wenn wir eine Saite zupfen, entstehen mehrere harmonische Grundschwingungen und ein paar nicht-harmonische Störschwingungen, die der Natur des Instruments geschuldet sind. Wir hören quasi ein „Bouqet“ aus Grundschwingungen. Wir als Menschen, nehmen deuten (zumindest oft) die dominanteste Schwingung als Grundfrequenz wahr. Die Aufgabe ist nun also diese Grundfrequenzen herauszufinden. Das ist eine sehr heikle Aufgabe, weil

die Amplituden der dominantesten Schwingungen sich kontinuierlich ändern
die dominanteste Schwingung sich im Laufe des Sample-Abschnitts ändern kann, (obwohl der ganze Sample auf eine Note deuten kann)

Die Anforderungen an einen Tuner können folgendermaßen zusammengefasst werden:

Aktualisierungsrate > $f_s=10Hz$
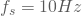
Minimale Frequenz: $f_{min}=27,5Hz (A0)$
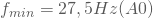
Maximale Frequenz= $f_{max}=440Hz (A4)$
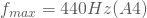
Messgenauigkeit:= $\Delta_{max}=1cent$
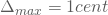
Effiziente Berechnung (abhängig vom eingesetzten DSP)

Mathematische Ansätze

Es gibt verschiedene mathematische Ansätze für die Umsetzung der Frequenzbestimmung:

Fourier-Transformation
Hartley-Transformation
Auto-Correlation
…

Die Fourier und Hartley-Transformationen basieren auf den Ansatz, dass man das Signal erst in Frequenzbereich transformiert und das Frequenzspektrum ermittelt. Für niedrige Frequenzen kann das eine geeignete Methode sein, um 1 Cent Genauigkeit zu erreichen. Allerdings wird die Transformation sehr langsam, wenn wir das Spektrum über mehrere 100Hz mit Hundertstel-Hertz-Genauigkeit ermitteln wollen. Denn die Genauigkeit der Fourier-Transformation müssen wir über das ganze Spektrum festlegen. Anders bei der Auto-Korrelation:

Auto Korrelation

Das Prinzip der Auto-Korrelation (Selbst-Übereinstimmung) ist relativ einfach. Wir multiplizieren unser Signal mit sich selbst mit einem zeitlichen Offset. Danach erhalten wir einen skalaren Wert. Dieser Wert gibt uns eine quantitative Aussage darüber, wie das Signal bei diesem Offset mit sich selbst übereinstimmt. Wenn wir dann die Offsets finden, bei denen die Korrelation am Höchsten ist, können wir daraus die Frequenzen ermitteln. Die Frequenz wäre dann einfach der Kehrwert vom Offset.

Der Algorithmus sieht folgendermaßen aus:

(1) $\begin{equation*} AC(\delta)=\sum_{i=1}^{n} y(i) \cdot y(i-\delta) \end{equation*}$

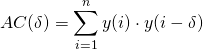
oder wenn das Signal im Puffer vorliegt, auch vorwärts berechnend:

(2) $\begin{equation*} AC(\delta)=\sum_{i=1}^{n} y(i) \cdot y(i+\delta) \end{equation*}$

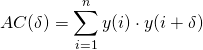
Dann erhalten wir einen Auto-Korrelationswert $AC$ für das Offset $\delta$ . Die Anzahl der Samples $n$ , über die wir diesen Wert berechnen muss

so groß wie möglich sein, um niedrige Frequenzen abbilden zu können und
so klein wie möglich sein, um die Anzahl der Multiplikationen zu reduzieren.

Wenn wir bei der Messung von $f_{max}=440Hz$ eine Genauigkeit von 1 cent haben wollen, bedeutet das eine Frequenzgenauigkeit $F_{\Delta}$

(3) $\begin{equation*} F_{\Delta}=440 \cdot 2^{\frac{1}{1200}}-440=0.254Hz \end{equation*}$

Auf der anderen Seite, wenn wir tiefe Frequenzen gut auflösen wollen, brauchen wir einen Sampleabschnitt, der ein paar volle Schwingungen beinhaltet. Bei 4 mal 20Hz Schwingungen ergibt sich eine Sample-Anzahl von

(4) $\begin{equation*} n_{27,5Hz}=48000/27,5 \cdot 4= 6981 \end{equation*}$

Also wenn wir den ganzen Frequenzbereich mit 0,3Hz Genauigkeit scannen und daraus die Autokorrelation von allen Frequenzen mit 9600 Samples berechnen, beträgt der Rechenaufwand

(5) $\begin{equation*} O_{MAC}=[(440-27,5)/0.28] 6981=10284508 \end{equation*}$

Multiplikation und Additionen. Das bedeutet rund 10,2Mio. Operationen pro Scan. Bei einer Aktualisierungsrate von $f_S=10Hz$ brauchen wir 200Mio. Rechenoperationen pro Scan – nur um Autokorrelationswerte zu berechnen. Also dieser primitiver Ansatz ist nicht geeignet, um die Frequenz auf eine effiziente Weise zu berechnen.

Ein effizienter Ansatz zur Frequenzbestimmung

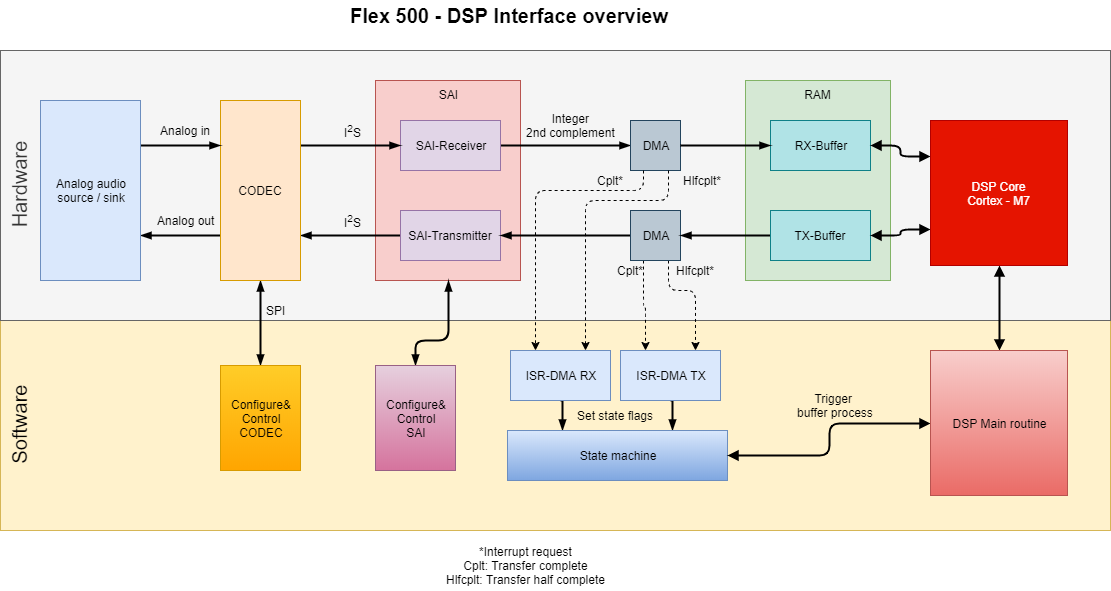
Wenn wir nur an ein paar dominanten Frequenzen interessiert sind, müssen wir nicht die Auto-Korrelationswerte für das ganze Spektrum mit feiner Auflösung berechnen. Daraus entstehen einige Optimierungsansätze: Man kann erst den groben Bereich der dominanten Frequenzen berechnen und dann diese in dem Bereich suchen. Dieser Ansatz ist im unteren Diagramm dargestellt.

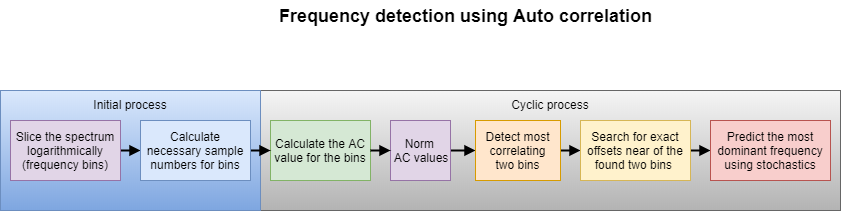
Die einzelnen Schritte dieses Ansatzes ist im Folgenden erklärt.

Das Spektrum RASTERN

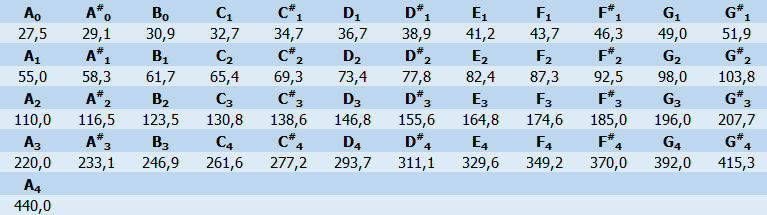
Zuerst wollen wir das Spektrum zwischen A0 und A4, also 27,5Hz und 440Hz in so wenig wie möglich Raster teilen, bei denen wir uns sicher sind, dass nicht mehrere dominante Frequenzen drin vorkommen können. Im vorliegenden Fall möchten wir die dominante Frequenz eines Musikinstruments, konkreter Gitarre und Bassgitarre ermitteln. Für den Zweck bietet es sich an, die chromatischen Notenfrequenzen als Raster zu nehmen. Unten sind die Noten von 27,5Hz bis 440 Hz dargestellt.

Notenfrequenzen

Das heißt, wir können das Spektrum, dass uns interessiert, erstmal in 49 Blöcke teilen. Dann berechnen wir nur den AC-Wert, der uns interessiert. Wir ermitteln hier die Information: „Um welche Note geht’s denn überhaupt?“

Zudem: Die Wahl der Noten nach chromatischen Frequenzen bei 440Hz-Stimmung, ist auch eine strategische Wahl. Denn: Die gefundenen Noten aus diesem Array werden genommen, um in ihrer Nähe nach der exakten Frequenz zu suchen. Diese Noten sind auch die erste Schätzung für die Suche. Mit der Annahme, dass dieser Algorithmus als chromatischer Tuner bei einem 440Hz-gestimmten Instrument benutzt werden soll, erwarten wir oft eine Übereinstimmung in unmittelbarer Nähe.

Zunächst werden diese Frequenzen als Offsets $\delta$ in einem Array gespeichert:

(6) $\begin{equation*} \delta(f)=f_s/f \end{equation*}$

Wir denken ab nun nicht mehr in Frequenzen $f$ sondern in Offsets $\delta$ .

static const unsigned s_bins=49;
unsigned note_bins[s_bins]={1745,1647,1555,1467,1385,...

1 2	static const unsigned s_bins=49; unsigned note_bins[s_bins]={1745,1647,1555,1467,1385,...

Erforderliche Sample-Anzahl 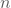$n$ für die Raster berechnen

Wie bereits erwähnt, brauchen wir bei tieferen Frequenzen mehr Samples für die Auto-Korrelation-Berechnung als bei höheren Frequenzen. Dafür muss man sich eine Art Güte ausdenken. Wenn man sich z.B. für eine Güte von 4 vornimmt, bedeutet das, dass man 4 volle Schwingungen einer Frequenz für die Auto-Korrelationsberechnung braucht. Das ergibt

(7) $\begin{equation*} n(\delta)=[f_s/f] \psi \end{equation*}$

bei der Güte $\psi$ .

Die Implementierung würde folgendermaßen aussehen:

	unsigned l_acbuf;
	unsigned l_max;

	//Length of samples we need
	l_acbuf=n_waves_ac*dist;
	l_max=bufsize-dist;

	if(l_acbuf>l_max){
		l_acbuf=l_max;
	}

unsigned l_acbuf;

unsigned l_max;

//Length of samples we need

l_acbuf=n_waves_ac*dist;

l_max=bufsize-dist;

if(l_acbuf>l_max){

l_acbuf=l_max;

}

Auto-Korrelationswert berechnen

Die Berechnung vom Auto-Korrelationswert ist oben beschrieben. Je nach Hardwareressourcen kann dies z.B. folgendermaßen implementiert werden.

ac_score=0;
for(i=0;i<l_acbuf;i++){
    ac_score+=buffer[i]*buffer[i+dist];
}

ac_score=0;

for(i=0;i<l_acbuf;i++){

ac_score+=buffer[i]*buffer[i+dist];

}

Auto-Korrelationswert normieren

Wir haben variable Anzahl an Samples für jede Frequenz, da wir erstens tiefe Frequenzen erfassen können, andererseits bei höheren Frequenzen Ressourcen sparen wollen. Daraus ergeben sich Auto-Korrelationswerte, die nicht untereinander vergleichbar sind. Wir normieren diese deshalb nach der Länge der Samples, mit denen sie berechnet wurden. Damit kann man die Amplituden einzelner Raster miteinander vergleichen.

//Norming AC Score: Divide by the count of the samples
     ac_score=ac_score/l_acbuf;

1 2	//Norming AC Score: Divide by the count of the samples ac_score=ac_score/l_acbuf;

Extrema des Spektrums (PEAKS) ermitteln

Jetzt haben wir das Spektrum, d.h. die AC-Werte für jeden Rasterpunkt, ermittelt. Wir müssen nun dort herausfiltern, welche Offsets wir brauchen. Dieser Teil ist etwas „tricky“ und beruht auf folgenden Erfahrungswerten für Gitarren und Bass-Stimmung:

Bei einer Einzelsaite entstehen u. a. zwei deutlich dominante Peaks.
Die Peaks sind die ersten Harmonischen voneinander ( $f_1/f_2=2$ )
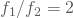Die Amplituden der beiden Peaks sind sehr ähnlich und wechseln sich oft beim Ausklingen.
Der tiefere Peak ist aussagekräftiger, da man dadurch die Frequenz (ohne Oversampling) präziser messen kann (n_2>n_1)

Deshalb versuchen wir im folgenden Schritt

Zwei dominanteste Offsets (Peaks) aussuchen
Diese sortieren

Das wird folgendermaßen implementiert.

void c_tuner::find_peaks(void){

	p1=0;
	p2=0;


	unsigned n_peak;	//Peak count
	unsigned i;
	//Finding the peaks
	n_peak=0;											//Number of found peaks
		for(i=1; i<s_bins-1;i++){
			if(arr_ac[i]>0){								//Find only positive peaks
				if(arr_ac[i]>arr_ac[i-1] && arr_ac[i]>arr_ac[i+1]){	//Peak found
//					printf("Peak found:%f \t%f\n",(float)(FS/note_bins[i]),arr_ac[i]);
					n_peak++;								//Number of found peaks
					if(n_peak==1){							//Check if the found peak is the first peak
						p1=i;							//Initialize first peak (distance)
					}else if(n_peak==2){					//Check if the found peak is the second peak
						p2=i;							//Initialize second peak (distance)
					}

					if(arr_ac[p1]<arr_ac[i]){			//If the current peak distance is greater than the last peak distance
						p2=p1;						//Update the peak distances: Shift the next greatest to the second place
						p1=i;							//Set the greatest
					}else if(arr_ac[p2]<arr_ac[i]){		//If the current peak distance is greater than the second peak distance
						p2=i;							//Update the second peak
					}
				}
			}
		}

}

void c_tuner::find_peaks(void){

p1=0;

p2=0;

unsigned n_peak; //Peak count

unsigned i;

//Finding the peaks

n_peak=0; //Number of found peaks

for(i=1; i<s_bins-1;i++){

if(arr_ac[i]>0){ //Find only positive peaks

if(arr_ac[i]>arr_ac[i-1] && arr_ac[i]>arr_ac[i+1]){ //Peak found

// printf("Peak found:%f \t%f\n",(float)(FS/note_bins[i]),arr_ac[i]);

n_peak++; //Number of found peaks

if(n_peak==1){ //Check if the found peak is the first peak

p1=i; //Initialize first peak (distance)

}else if(n_peak==2){ //Check if the found peak is the second peak

p2=i; //Initialize second peak (distance)

}

if(arr_ac[p1]<arr_ac[i]){ //If the current peak distance is greater than the last peak distance

p2=p1; //Update the peak distances: Shift the next greatest to the second place

p1=i; //Set the greatest

}else if(arr_ac[p2]<arr_ac[i]){ //If the current peak distance is greater than the second peak distance

p2=i; //Update the second peak

}

Nach den exakten Frequenzen (Offsets) suchen

Wir haben nun zwei Frequenzen ermittelt, bei denen wir wissen, unsere gesuchte Frequenz liegt in deren unmittelbare Nähe. Man kann sich das ungefähr folgendermaßen vorstellen:

Rendered by QuickLaTeX.com

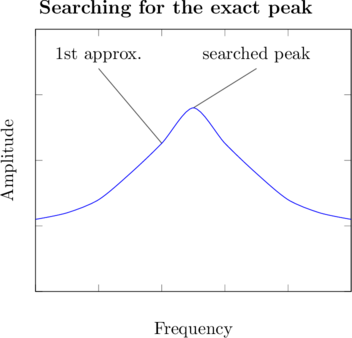
Es existieren zahlreiche Suchalgorithmen. Je nach Anwendung können diese Vor- und Nachteile haben. Eine Übersicht ist hier verfügbar. In dem Fall bieten sich hauptsächlich zwei Suchalgorithmen

Die Wahl zwischen diesen Algorithmen sind im vorliegenden Fall schwierig. Wenn die gesuchte Frequenz in der Ferne liegt, ist binäre Suche vorteilhafter. Wenn diese aber in der Nähe liegt, ist lineare Suche vorteilhafter.

Die Implementierung dieser Suche ist folgendermaßen zu realisieren:

unsigned c_tuner::get_exact_peak_linear(unsigned index){


	unsigned dist=note_bins[index];


	float ac_prev=calc_ac(dist-1);
	float ac=arr_ac[index];
	float ac_next=calc_ac(dist+1);

	unsigned n=0;		//Loop counter
	unsigned n_exit=100;	//Emergency exit

	//Get gradient
	while(n<n_exit){
		n++;

		if(ac>=ac_prev){

			if(ac<ac_next){
				//Gradient positive
				dist++;
				ac_prev=ac;
				ac=ac_next;
				ac_next=calc_ac(dist+1);

			}else if(ac>=ac_next){
				//Found peak
				break;
			}
		}else if(ac<ac_prev){
			//Gradient negative
			if(ac>=ac_next){
				dist--;
				ac_next=ac;
				ac=ac_prev;
				ac_prev=calc_ac(dist-1);
			}else{
				//Negative peak
				dist=0;
				break;
			}

		}

	}
	return dist;
}

unsigned c_tuner::get_exact_peak_linear(unsigned index){

unsigned dist=note_bins[index];

float ac_prev=calc_ac(dist-1);

float ac=arr_ac[index];

float ac_next=calc_ac(dist+1);

unsigned n=0; //Loop counter

unsigned n_exit=100; //Emergency exit

//Get gradient

while(n<n_exit){

n++;

if(ac>=ac_prev){

if(ac<ac_next){

//Gradient positive

dist++;

ac_prev=ac;

ac=ac_next;

ac_next=calc_ac(dist+1);

}else if(ac>=ac_next){

//Found peak

break;

}

}else if(ac<ac_prev){

//Gradient negative

if(ac>=ac_next){

dist--;

ac_next=ac;

ac=ac_prev;

ac_prev=calc_ac(dist-1);

}else{

//Negative peak

dist=0;

break;

}

return dist;

}

Stochastische Abschätzung der GESUCHTEN Frequenz

Nachdem die exakten zwei Frequenzen ermittelt wurden, merkt man, dass dieser Wert in einem kleinen Intervall schwankt, was der Natur der Instrumente geschuldet ist. Nun muss

die Plausibilität der berechneten Frequenzen bewertet und
der Frequenzverlauf gemittelt werden,

damit der Benutzer eine vernünftige Frequenz- bzw. Notenanzeige hat. Dafür wird eine Toleranz $\sigma$ eingeführt, innerhalb dessen die Frequenz schwanken darf. Wenn eine Messung diese Toleranz überschreitet, vermutet man ein Notenwechsel. Also entweder wird eine andere Saite gezupft oder so stark korrigiert, dass man diese Messung nicht mehr in die Mittelung einfließen darf. Danach wird die Mittelung zurückgesetzt und weiterhin auf eine Messungfolge gewartet, wo alle Messungswerte innerhalb der Toleranz liegen. Danach wird die Note wieder gezeigt.

Die Implementierung kann folgendermaßen aussehen:

/*This function uses methods of stochastics to estimate the frequency*/
void c_tuner::estimate_freq(void){

	float ma;					//Value of moving average
	float minimum, maximum;		//Minimum and maximum values of one array
	double deviation;			//Current deviation in the array
	float fin;



	fin=(float)FS/(float)p;		//Input frequency

	//Moving average filter

	//Insert value
	buf_maf[maptr]=fin;

	//Update pointer
	maptr++;

	if(maptr>=l_maf){
		maptr=0;
	}

	//Calculate moving average

	ma=0;
	minimum=buf_maf[0];
	maximum=buf_maf[0];

	unsigned i=0;
	for(i=0;i<l_maf;i++){
		//Update moving average
		ma+=buf_maf[i];

		//Find the minimum value of array
		if(buf_maf[i]<minimum){
			minimum=buf_maf[i];
		}

		//Find the minimum value of array
		if(buf_maf[i]>maximum){
			maximum=buf_maf[i];
		}
	}

	//Moving average value
	ma=ma/l_maf;

	//Deviation
	deviation=maximum/minimum;

	//Check if deviation is within the tolerance band
	if(deviation<=devtol){		//Note confidence good=>Everything fine
		last_conf_f=ma;

//		last_conf_t=HAL_GetTick(); //Commented out for Win
		fc=ma;

	}else{												//Note confidence bad => Set a timer
//		if((HAL_GetTick()-last_conf_t)<conf_timeout){ //Commented out for Win
		if(1){
			fc=last_conf_f;

		}else{
			//Timeout
			last_conf_f=0;
			last_conf_t=0;
			fc=0;
		}

	}

	printf("Fc=%.2f\n",fc);

}

/*This function uses methods of stochastics to estimate the frequency*/

void c_tuner::estimate_freq(void){

float ma; //Value of moving average

float minimum, maximum; //Minimum and maximum values of one array

double deviation; //Current deviation in the array

float fin;

fin=(float)FS/(float)p; //Input frequency

//Moving average filter

//Insert value

buf_maf[maptr]=fin;

//Update pointer

maptr++;

if(maptr>=l_maf){

maptr=0;

}

//Calculate moving average

ma=0;

minimum=buf_maf[0];

maximum=buf_maf[0];

unsigned i=0;

for(i=0;i<l_maf;i++){

//Update moving average

ma+=buf_maf[i];

//Find the minimum value of array

if(buf_maf[i]<minimum){

minimum=buf_maf[i];

}

//Find the minimum value of array

if(buf_maf[i]>maximum){

maximum=buf_maf[i];

}

//Moving average value

ma=ma/l_maf;

//Deviation

deviation=maximum/minimum;

//Check if deviation is within the tolerance band

if(deviation<=devtol){ //Note confidence good=>Everything fine

last_conf_f=ma;

// last_conf_t=HAL_GetTick(); //Commented out for Win

fc=ma;

}else{ //Note confidence bad => Set a timer

// if((HAL_GetTick()-last_conf_t)<conf_timeout){ //Commented out for Win

if(1){

fc=last_conf_f;

}else{

//Timeout

last_conf_f=0;

last_conf_t=0;

fc=0;

}

printf("Fc=%.2f\n",fc);

}

Ressourcen

Hiermit wurde der Ablauf einer Frequenzermittlung für eine Tuner-Applikation gezeigt. Der vollständige Target-Code für DSP und der Simulationscode für Windows kann vom GitHub heruntergeladen werden.

Digitaler Tuner (Stimmgerät)

Ein Effektgerät besteht hauptsächlich aus den Komponenten

Im Falle von einem verteilten System wird die Frequenzerkennung auf dem DSP durchgeführt. Die erkannte Frequenz wird dem Controller mitgeteilt, der dann Korrektur-/Stimmhilfe gibt. Dazu gehört

die Erkennung/Vermutung der Soll-Note
Die Abweichung von der vermuteten Soll-Note.

Die Erkennung der Frequenz bzw. die Darstellung der Abweichung ist in obigen Kapiteln ausführlich beschrieben.

DSP Architektur

11. Dezember 2019 / solocan / Noch kein Kommentar

Ein DSP-FX benötigt jitter-freie Verarbeitung der Audiodaten in Echtzeit. Echtzeit ist ein theoretischer und dehnbarer Begriff, der die erforderliche Systemlatenz beschreibt. Beim Audio beruht diese Feststellung auf die Latenzwahrnehmung des Menschen. Wir nehmen die Latenzen unter 10ms als Echtzeit wahr. Die Latenz der gesamten Kette (Roundtriplatenz) ist die Zeit zwischen dem Eintreten des Signals in die Codec-Eingänge bis zur Bereitstehung des verarbeiteten Signals an Codec-Ausgängen. Diese Zeit darf 10ms nicht überschreiten. Am besten soll diese Zeit sogar noch unter 10ms liegen, da auch der Schall zwischen den Lautsprechern und dem Ohr zusätzlich große Latenz erzeugt und Echtzeiterlebnis schnell beeinflusst werden kann.

Systemarchitektur

Die Übersicht der Systemarchitektur des DSPs vom Flex 500 ist im folgenden Diagramm gezeigt:

Codec

Ein Audio- Codec (Coder, decoder) ist die Komponente, die die analogen Audio-Signale ins Digitale wandelt und die digitalen Audio-Signale ins Analoge wandelt. (Sampling) Er besteht aus einem oder mehreren Analog-Digital-Wandlern (ADC) und ein Digital-Analog-Wandlern (DAC). Nach diesem Schritt liegen die Audio-Signale in einem digitalen Audio-Format vor, im vorliegenden Fall als I2S-Format (Intersound).

Die Codecs müssen konfiguriert und initialisiert werden. Das erfolgt über eine andere serielle Schnittstelle, üblicherweise SPI oder I2C. Das heißt, der Codec hat auch eine Steuerschnittstelle zum DSP. Beim Flex 500 stehen beide Schnittstellen zur Verfügung.

SAI

SAI (Serial Audio Interface) ist eine Schnittstelle, über die digitale Audio-Daten ausgetauscht werden können. Der Codec kommuniziert mit der SAI-Schnittstelle vom DSP-Chip, in dem Fall STM32H743. Diese Schnittstelle serialisiert und deserialisiert die Audiodaten, D.h. er schreibt/liest die in den bzw. von dem Arbeitsspeicher.

DMA

Das Schreiben bzw. Lesen muss über eine DMA (DIrect memory access)-Hardware-Komponente erfolgen. DMA ist eine einfache Hardware, die die Aufgabe hat, ein Register in das andere zu kopieren. Die Startaddresse, FIFO, IRQs und die Länge müssen dabei konfiguriert werden. Dadurch dass DMA die Datenübertragungsaufgabe übernimmt, kann sich DSP auf die Datenverarbeitung konzentrieren.

DMA muss so konfiguriert werden, dass er ein Interrupt auslöst, wenn die Puffer

halb voll und
ganz voll

sind. Dadurch können die Flags der Zustandsmaschine (State machine) gesetzt werden.

Puffer

Das vom Audio-Codec ins digitale I2S-Format gewandelte Audio-Signal muss in einem Eingangspuffer zwischengespeichert werden. Dann wird dieses Puffer vom DSP verarbeitet und das Ergebnis in ein Ausgangspuffer geschrieben. Die Größe der Puffer ergibt sich aus dem Kompromiss aus zwei Anforderungen:

Die Puffer muss so klein wie möglich sein, um eine nicht-wahrnehmbare Latenz zu erreichen.
Die Puffer müssen so groß wie möglich sein, um eine effiziente blockweise Datenverarbeitung zu ermöglichen (Overhead muss reduziert werden)

Bei den Anforderungen

Roundtrip-Latenz = 10ms
Abtastrate $f_S$ = 48kHz
Bittiefe = 32bit

ergibt sich eine Puffergröße von 240 für jeweils Eingangs- und Ausgangspuffer mit 32bit Registern, da Eingangslatenz und Ausgangslatenz 5ms betragen müssen.

Für die Verarbeitung mit DMA-Interrupts wird ein Doppelpuffer der Größe 480 verwendet. Für genaue Erkläreung, siehe unten.

Zustandsmaschine

Die Zustandsmaschine ist die Hauptsteuerungskomponente in der Software. Durch die Interrupts von DMA wird der Software mitgeteilt, dass das Puffer halb oder ganz voll ist. Nun kann die Zustandsmaschine, die in Endlosschleife läuft, entscheiden, ob der Prozess getriggert werden soll.

Die auf STM32 eingesetzter DMA unterstützt Double-buffering. Das heißt, er kann auf der Hälfte und am Ende der Übertragung ein Interrupt auslösen. Deshalb müssen wir das Doppelpuffer nicht selbst managen.

Der Ablauf sieht folgendermaßen aus:

Erste Hälfte vom RX fertig ( Ab nun beschreibt DMA die zweite Hälfte)
Erste Hälfte vom TX fertig ( Ab nun beschreibt DMA die zweite Hälfte)
Zustandsmaschine löst die Verarbeitung der ersten Hälfte aus. Jetzt liest DSP von der ersten Hälfte von RX und beschreibt die erste Hälfte von TX.
Zweite Hälfte vom RX fertig ( Ab nun beschreibt DMA die erste Hälfte)
Zweite Hälfte vom TX fertig ( Ab nun beschreibt DMA die erste Hälfte)
Zustandsmaschine löst die Verarbeitung der zweiten Hälfte aus. Jetzt liest DSP von der zweiten Hälfte von RX und beschreibt die zweite Hälfte von TX.
Zurück zu 1.

Man erkennt, dass zwischen den RX und TX interrupts ein kleiner Versatz ist. Zwar synchronisiert der Codec die ADCs und DACs aber trotzdem entstehen ein kleines Offset von ein paar Samples. Um den Jitter zu verhindern, müssen beide Interrupts ausgewertet werden, um sicherzugehen, dass in der zu verarbeitenden Hälfte wirklich nichts mehr beschrieben bzw. gelesen wird.

Implementierung

Zuerst müssen die Stati initialisiert werden.

/*Init routine*/
void c_ser::init(void){

	tx_status=0;
	rx_status=0;


	//Initialize DSP
	dsp.init();

}

/*Init routine*/

void c_ser::init(void){

tx_status=0;

rx_status=0;

//Initialize DSP

dsp.init();

}

Die Hauptroutine, die Endlosschleife der Verarbeitung wird folgendermaßen implementiert:

/*
 * Main loop for the state machine
 * */
void c_ser::start(void){

	bool old_pos=1;
	unsigned i;
	//Endless main loop
	while(1){

		if((tx_status && rx_status)&&old_pos){ //When pointer is on the second half of the buffer

			for(i=0;i<buf_size*2;i+=2){
				tx_buf[i]=dsp.process(&rx_buf[i]); //(mono right)

			}
			old_pos=0;

		}else if(!(tx_status || rx_status)&&!old_pos){//When pointer is on the first half of the buffer

			for(i=buf_size*2;i<buf_size*4;i+=2){
				tx_buf[i]=dsp.process(&rx_buf[i]); //(mono right)
			}
			old_pos=1;
		}else{
			//Can measure idle here
		}

	}
}

* Main loop for the state machine

* */

void c_ser::start(void){

bool old_pos=1;

unsigned i;

//Endless main loop

while(1){

if((tx_status && rx_status)&&old_pos){ //When pointer is on the second half of the buffer

for(i=0;i<buf_size*2;i+=2){

tx_buf[i]=dsp.process(&rx_buf[i]); //(mono right)

}

old_pos=0;

}else if(!(tx_status || rx_status)&&!old_pos){//When pointer is on the first half of the buffer

for(i=buf_size*2;i<buf_size*4;i+=2){

tx_buf[i]=dsp.process(&rx_buf[i]); //(mono right)

}

old_pos=1;

}else{

//Can measure idle here

}

Die Flags tx_status und rx_status wurden in Interrupt Routinen gesetzt und hier (nach der Verarbeitung) wieder geresettet.

void HAL_SAI_TxCpltCallback(SAI_HandleTypeDef *hsai)
{
	tx_status=0;
}

void HAL_SAI_TxHalfCpltCallback(SAI_HandleTypeDef *hsai){
	tx_status=1;
}

void HAL_SAI_RxCpltCallback(SAI_HandleTypeDef *hsai){
	rx_status=0;
}

void HAL_SAI_RxHalfCpltCallback(SAI_HandleTypeDef *hsai){
	rx_status=1;
}

void HAL_SAI_TxCpltCallback(SAI_HandleTypeDef *hsai)

{

tx_status=0;

}

void HAL_SAI_TxHalfCpltCallback(SAI_HandleTypeDef *hsai){

tx_status=1;

}

void HAL_SAI_RxCpltCallback(SAI_HandleTypeDef *hsai){

rx_status=0;

}

void HAL_SAI_RxHalfCpltCallback(SAI_HandleTypeDef *hsai){

rx_status=1;

}

Wichtig: Die Interruptroutine muss so schnell wie möglich ablaufen, da diese höchste Priorität hat und alles pausiert. Hier nichts verarbeiten, sondern nur Flags setzen, die dann in der Hauptschleife verarbeitet werden.

WM8731 CODEC-Schnittstelle für Nucleo H743

7. Dezember 2019 / solocan / Noch kein Kommentar

Die WM8731 ist ein Budget-Klasse-Stereo Audio-CODEC von Cirrus Logic für mobile Applikationen. Es unterstützt 24bit Bittiefe, bis zu 96kHzAbtastrate und besitzt einen dynamischen Bereich vom 90db für ADC und 100dB für DAC .

Für Flex 500 wurde ein Breakout-Board für WM8731 entwickelt, das man direkt auf ein Nucleo Board stecken kann.

Board-Design

Folgendes auf Referenzdesign basiertes Design wurde für das Breakout board entwickelt.

Analoge Ein- und Ausgänge

Da WM8731 für mobile Anwendungen mit knappem Platz entwickelt ist, kommt es ohne zusätzlichen Eingangs- und Ausgangsstufen klar. Dafür unterstützt es nur unsymmetrische Ein- und Ausgänge.

Dafür hat es einen integrierten Kopfhörerverstärker. Auf dem Board befinden sich Line-In/Out und Kopfhörer-Anschlüsse.

Oszillator

Ein 24,576 MHz Oszillator ist eingebaut und gibt den Takt an den Master-Clock.

Ressourcen

Die KiCad Schaltung- und PCB-Designdaten herunterladen

Kompletter Programmcode für H743-Target

CS4272 CODEC-Schnittstelle für Nucleo H743

7. Dezember 2019 / solocan / Noch kein Kommentar

Die CS4272 ist ein hochwertiges Stereo Audio-CODEC von Cirrus Logic für anspruchsvolle Implementierungen. Es unterstützt 24bit Bittiefe, bis zu 192kHz Abtastrate und besitzt einen dynamischen Bereich vom 114dB.

Für Flex 500 wurde ein Breakout-Board für CS4272 entwickelt, das man direkt auf ein Nucleo Board stecken kann.

PCB Design

CS4272 CODEC- Breakout board im Betrieb

Board-Design

CS4272 unterstützt 2x symmetrische Eingänge und hat 2x symmetrische Ausgänge.

Symmetrische Eingänge

Die Nutzsignale vom analogen Preamp-Board sind Wechselspannungen, da Preamp-Board symmetrische Spannungsversorgung von $+-15V$ hat. Für die symmetrischen Eingänge muss das Signal vom Preamp-Board in einen Pegel von $V_{pp}<5V$ gebracht werden. Danach muss eine Gleichspannung $V_{alias}=2,5V$ addiert werden, damit das Eingangssignal in den erlaubten Bereich vom CS4272 $0V\leq V_{i} \leq5V$ gebracht werden. Das wird in der untenstehenden Schaltung realisiert:

Bei diesem Design handelt es sich um das Referenzdesign von CS4272. Hierbei wird die Alias-Spannung $V_{com}=2,5V$ auf die durch die Kondensatoren C_INAx entkoppelte Eingangsspannung addiert und ein Eingangspuffer hinzugefügt.

Symmetrische Ausgänge

Die analogen Ausgänge vom CS4272 symmetrisch und für weitere Verarbeitung desymmetriert werden. Das wurde mit folgender Schaltung realisiert.

Hierbei werden die symmetrischen Signale $V_{OUT,A+}$ und $V_{OUT,A-}$ in einer Stufe voneinander abgezogen. Danach wird mit dem Ausgangskondesator C_OUTA6 der Gleichstrom herausgefiltert. Schließlich arbeitet die ganze Schaltung auf einen Lastwiderstand von $R_L=47k\Omega$ . Hierbei handelt es sich um das Referenz Design von CS4272.

Digitale Schnittstellen

Das Breakout-Board unterstützt SPI und I2C Schnittstellen zum Controller.

Initialisierungssequenz

Die Initialisierungssequenz von CS4272 ist im folgenden Code gezeigt.

void cs4272::init(void){


	//Initialize SPI
	printf("Initing SPI5\n");
	MX_SPI5_Init();


	printf("Initing codec\n");

	HAL_GPIO_WritePin(GPIOG,GPIO_PIN_0,(GPIO_PinState)0); //RST low

		uint8_t i=0;
		uint8_t reg[8][3];
		uint8_t adr=0b00100000;

		//Init address
		for(i=0;i<sizeof(reg)/3;i++){
			reg[i][0]=adr;
		}

		//Define startup sequence
		reg[0][1]=0x7; //Power down control
		reg[0][2]=0b00000011; //Set Serial mode + power down

		reg[1][1]=0x1; //Mode control 1
		reg[1][2]=0b00101001; //48kHz Master

		reg[2][1]=0x2;	//DAC Control
		reg[2][2]=0b00000000;

		reg[3][1]=0x3; //DAC Volume control
		reg[3][2]=0b00001001;

		reg[4][1]=0x4;	//DAC Volume A
		reg[4][2]=0b10000000; //No mute + 0dB

		reg[5][1]=0x5;	//DAC Volume B
		reg[5][2]=0b10000000; //No mute + 0dB

		reg[6][1]=0x6;	//ADC Control
		reg[6][2]=0b00010000;

		reg[7][1]=0x7;	//Mode control 2
		reg[7][2]=0b00001010;
	//	reg[7][2]=0b00010010;//Loop ADC->DAC


		HAL_GPIO_WritePin(GPIOG,GPIO_PIN_1,(GPIO_PinState)1); //MS high: SPI Unselect device
		HAL_GPIO_WritePin(GPIOG,GPIO_PIN_0,(GPIO_PinState)1); //RST High
		HAL_Delay(2); //Wait
		//HAL_GPIO_WritePin(GPIOG,GPIO_PIN_0,0); //RST Low

		for(i=0;i<sizeof(reg)/3;i++){
			HAL_GPIO_WritePin(GPIOG,GPIO_PIN_1,(GPIO_PinState)0); //MS low: SPI Select device
			HAL_SPI_Transmit(&hspi5,(uint8_t *)&reg[i],3,1000); //Send config register
			HAL_GPIO_WritePin(GPIOG,GPIO_PIN_1,(GPIO_PinState)1);//MS high: SPI Unselect device
			HAL_Delay(1); //Wait

		}
}

void cs4272::init(void){

//Initialize SPI

printf("Initing SPI5\n");

MX_SPI5_Init();

printf("Initing codec\n");

HAL_GPIO_WritePin(GPIOG,GPIO_PIN_0,(GPIO_PinState)0); //RST low

uint8_t i=0;

uint8_t reg[8][3];

uint8_t adr=0b00100000;

//Init address

for(i=0;i<sizeof(reg)/3;i++){

reg[i][0]=adr;

}

//Define startup sequence

reg[0][1]=0x7; //Power down control

reg[0][2]=0b00000011; //Set Serial mode + power down

reg[1][1]=0x1; //Mode control 1

reg[1][2]=0b00101001; //48kHz Master

reg[2][1]=0x2; //DAC Control

reg[2][2]=0b00000000;

reg[3][1]=0x3; //DAC Volume control

reg[3][2]=0b00001001;

reg[4][1]=0x4; //DAC Volume A

reg[4][2]=0b10000000; //No mute + 0dB

reg[5][1]=0x5; //DAC Volume B

reg[5][2]=0b10000000; //No mute + 0dB

reg[6][1]=0x6; //ADC Control

reg[6][2]=0b00010000;

reg[7][1]=0x7; //Mode control 2

reg[7][2]=0b00001010;

// reg[7][2]=0b00010010;//Loop ADC->DAC

HAL_GPIO_WritePin(GPIOG,GPIO_PIN_1,(GPIO_PinState)1); //MS high: SPI Unselect device

HAL_GPIO_WritePin(GPIOG,GPIO_PIN_0,(GPIO_PinState)1); //RST High

HAL_Delay(2); //Wait

//HAL_GPIO_WritePin(GPIOG,GPIO_PIN_0,0); //RST Low

for(i=0;i<sizeof(reg)/3;i++){

HAL_GPIO_WritePin(GPIOG,GPIO_PIN_1,(GPIO_PinState)0); //MS low: SPI Select device

HAL_SPI_Transmit(&hspi5,(uint8_t *)&reg[i],3,1000); //Send config register

HAL_GPIO_WritePin(GPIOG,GPIO_PIN_1,(GPIO_PinState)1);//MS high: SPI Unselect device

HAL_Delay(1); //Wait

}

Nach der Initialisierung kann das CODEC aktiviert und deaktiviert werden.

void cs4272::set_status(bool flag){
	uint8_t mutereg[3];
	mutereg[0]=0b00100000;
	mutereg[1]=0x4; //DAC Volume control A register (MUTECA=B is on)

	if(flag){
		mutereg[2]=0b00000000;
	}else{
		mutereg[2]=0b10000000;
	}

	//Send SPI command to CODEC
	HAL_GPIO_WritePin(GPIOG,GPIO_PIN_1,(GPIO_PinState)0); //MS low: SPI Select device
	HAL_SPI_Transmit(&hspi5,(uint8_t *)&mutereg,3,1000); //Send config register
	HAL_GPIO_WritePin(GPIOG,GPIO_PIN_1,(GPIO_PinState)1);//MS high: SPI Unselect device
}

void cs4272::set_status(bool flag){

uint8_t mutereg[3];

mutereg[0]=0b00100000;

mutereg[1]=0x4; //DAC Volume control A register (MUTECA=B is on)

if(flag){

mutereg[2]=0b00000000;

}else{

mutereg[2]=0b10000000;

}

//Send SPI command to CODEC

HAL_GPIO_WritePin(GPIOG,GPIO_PIN_1,(GPIO_PinState)0); //MS low: SPI Select device

HAL_SPI_Transmit(&hspi5,(uint8_t *)&mutereg,3,1000); //Send config register

HAL_GPIO_WritePin(GPIOG,GPIO_PIN_1,(GPIO_PinState)1);//MS high: SPI Unselect device

}

Der SAI von H743 muss folgendermaßen konfiguriert sein:

void c_sai::MX_SAI1_Init(void)
{

  hsai_BlockA1.Instance = SAI1_Block_A;
  hsai_BlockA1.Init.AudioMode = SAI_MODESLAVE_RX;
  hsai_BlockA1.Init.Synchro = SAI_ASYNCHRONOUS;
  hsai_BlockA1.Init.OutputDrive = SAI_OUTPUTDRIVE_DISABLE;
  hsai_BlockA1.Init.FIFOThreshold = SAI_FIFOTHRESHOLD_EMPTY;
hsai_BlockA1.Init.AudioFrequency = SAI_AUDIO_FREQUENCY_48K;
  hsai_BlockA1.Init.SynchroExt = SAI_SYNCEXT_OUTBLOCKA_ENABLE;
  hsai_BlockA1.Init.MonoStereoMode = SAI_STEREOMODE;
  hsai_BlockA1.Init.CompandingMode = SAI_NOCOMPANDING;
  hsai_BlockA1.Init.TriState = SAI_OUTPUT_NOTRELEASED;
  if (HAL_SAI_InitProtocol(&hsai_BlockA1, SAI_I2S_STANDARD, SAI_PROTOCOL_DATASIZE_32BIT, 2) != HAL_OK)
  {
//    _Error_Handler(__FILE__, __LINE__);
  }

  hsai_BlockB1.Instance = SAI1_Block_B;
  hsai_BlockB1.Init.AudioMode = SAI_MODESLAVE_TX;
  hsai_BlockB1.Init.Synchro = SAI_SYNCHRONOUS;
  hsai_BlockB1.Init.OutputDrive = SAI_OUTPUTDRIVE_DISABLE;
  hsai_BlockB1.Init.FIFOThreshold = SAI_FIFOTHRESHOLD_EMPTY;
  hsai_BlockB1.Init.SynchroExt = SAI_SYNCEXT_DISABLE;
  hsai_BlockB1.Init.MonoStereoMode = SAI_STEREOMODE;
  hsai_BlockB1.Init.CompandingMode = SAI_NOCOMPANDING;
  hsai_BlockB1.Init.TriState = SAI_OUTPUT_NOTRELEASED;
  if (HAL_SAI_InitProtocol(&hsai_BlockB1, SAI_I2S_STANDARD, SAI_PROTOCOL_DATASIZE_32BIT, 2) != HAL_OK)
  {
//    _Error_Handler(__FILE__, __LINE__);
  }

}

void c_sai::start(void){

	//Start DMA Streams
	printf("Initializing SAI DMA Receive stream...\n");
//	printf("Initializing SAI DMA Receive stream...\n");
	HAL_SAI_Receive_DMA(&hsai_BlockA1, (uint8_t*)&rx_buf, 4*buf_size);
	printf("SAI DMA Receive stream initialized!\n");
//	printf("Initializing SAI DMA transmit stream...\n");
	HAL_SAI_Transmit_DMA(&hsai_BlockB1, (uint8_t*)&tx_buf, 4*buf_size);
	printf("SAI DMA transmit stream initialized!\n");

}

void c_sai::MX_SAI1_Init(void)

{

hsai_BlockA1.Instance = SAI1_Block_A;

hsai_BlockA1.Init.AudioMode = SAI_MODESLAVE_RX;

hsai_BlockA1.Init.Synchro = SAI_ASYNCHRONOUS;

hsai_BlockA1.Init.OutputDrive = SAI_OUTPUTDRIVE_DISABLE;

hsai_BlockA1.Init.FIFOThreshold = SAI_FIFOTHRESHOLD_EMPTY;

hsai_BlockA1.Init.AudioFrequency = SAI_AUDIO_FREQUENCY_48K;

hsai_BlockA1.Init.SynchroExt = SAI_SYNCEXT_OUTBLOCKA_ENABLE;

hsai_BlockA1.Init.MonoStereoMode = SAI_STEREOMODE;

hsai_BlockA1.Init.CompandingMode = SAI_NOCOMPANDING;

hsai_BlockA1.Init.TriState = SAI_OUTPUT_NOTRELEASED;

if (HAL_SAI_InitProtocol(&hsai_BlockA1, SAI_I2S_STANDARD, SAI_PROTOCOL_DATASIZE_32BIT, 2) != HAL_OK)

{

// _Error_Handler(__FILE__, __LINE__);

}

hsai_BlockB1.Instance = SAI1_Block_B;

hsai_BlockB1.Init.AudioMode = SAI_MODESLAVE_TX;

hsai_BlockB1.Init.Synchro = SAI_SYNCHRONOUS;

hsai_BlockB1.Init.OutputDrive = SAI_OUTPUTDRIVE_DISABLE;

hsai_BlockB1.Init.FIFOThreshold = SAI_FIFOTHRESHOLD_EMPTY;

hsai_BlockB1.Init.SynchroExt = SAI_SYNCEXT_DISABLE;

hsai_BlockB1.Init.MonoStereoMode = SAI_STEREOMODE;

hsai_BlockB1.Init.CompandingMode = SAI_NOCOMPANDING;

hsai_BlockB1.Init.TriState = SAI_OUTPUT_NOTRELEASED;

if (HAL_SAI_InitProtocol(&hsai_BlockB1, SAI_I2S_STANDARD, SAI_PROTOCOL_DATASIZE_32BIT, 2) != HAL_OK)

{

// _Error_Handler(__FILE__, __LINE__);

}

void c_sai::start(void){

//Start DMA Streams

printf("Initializing SAI DMA Receive stream...\n");

// printf("Initializing SAI DMA Receive stream...\n");

HAL_SAI_Receive_DMA(&hsai_BlockA1, (uint8_t*)&rx_buf, 4*buf_size);

printf("SAI DMA Receive stream initialized!\n");

// printf("Initializing SAI DMA transmit stream...\n");

HAL_SAI_Transmit_DMA(&hsai_BlockB1, (uint8_t*)&tx_buf, 4*buf_size);

printf("SAI DMA transmit stream initialized!\n");

}

Oszillator

Ein 24,576 MHz Oszillator ist eingebaut und gibt den Takt an den Master-Clock.

Ressourcen

SPICE-Simulationsdateien zu analogen Schnittstellen für CS4272 herunterladen

Die KiCad Schaltung- und PCB-Designdaten herunterladen

Kompletter Programmcode für H743-Target

Flex 500 – Analoge Schnittstellen

7. Dezember 2019 / solocan / Noch kein Kommentar

Flex 500 besitzt u. a. folgende Schnittstellen:

Kopfhörerausgang
Symmetrischen Eingang (Balanced in)
Symmetrischen Ausgang (Balanced out)

Kopfhörerausgang

Kopfhörer können sehr niedrige Impedanzen von bis zu $16\Omega$ haben. D.h. für den Kopfhörerausgang ist ein Verstärker erforderlich, der Lasten bis $16\Omega$ bei Ausgangspegeln von $V_{PP}=4V$ bedienen kann. Das bedeutet eine Effektivspannung von $V_{eff}=\frac{4}{\sqrt{2}}=2,828$ , was wiederum bei einer $R_L=16\Omega$ Last einer Effektivleistung von

(1) $\begin{equation*} P_{eff}=\frac{V_{eff}}{R_L}=\frac{2,828^2}{16}=0,5W \end{equation*}$

Das entspricht einer Leistung, für die die Kleinsignalverstärker bzw. Opamps nicht ausgelegt sind. Man kann dafür

einen diskreten Verstärker mit Transistoren bauen
einen Kopfhörer-IC verwenden
einen Strompuffer verwenden

Bei Flex 500 wurde ein Strompuffer von TI, der BUF634 verwendet. Die Schaltung mit dem Baxandall-Lautstärkenregler ist unten dargestellt.

Der Strompuffer wird in die Rückkopplungsschleife gesetzt. Die Anwendung des Strompuffers ist hier beschrieben.

Zudem besitzt Flex 500 eine Erkennung des eingesteckten Kopfhörersteckers. Wenn der Stecker eingesteckt ist, wird die Masse vom Optokopplereingang getrennt und der Transistor wird hochohmig. Mit Hilfe dieses Ausgangs kann an einem Mikrocontroller erkannt werden, ob Kopfhörer eingesteckt ist und automatisch den Leistungsverstärker ausschalten.

Symmetrischen Eingang

Für die Beschallung externe Audioquellen wurde bei Flex 500 einen symmetrischen Eingang eingebaut. Dieser basiert auf einen IC von Texas Instruments, dem INA134.

Die Umsetzung ist unten dargestellt.

Symmetrischer Ausgang

Für eine geräuscharme Aufnahme ist die symmetrische Übertragung der Audio-Signale unerlässlich. Deshalb wurde bei Flex 500 ein symmetrische Ausgang eingebaut. Dieser basiert auf einen IC von Texas Instruments, dem DRV135.

Die Umsetzung ist unten dargestellt.

Davor befindet sich ein Schalter, womit man die Signalquelle wählen kann, je nachdem ,ob man vor oder nach der Signalverarbeitung aufnehmen möchte.

Ground lift

Die symmetrischen Leitungen zeichnen sich aus zwei wichtigsten Gründen aus

Die Störungen wirken auf beide Kabelader $V_O$ und $V_{O,inv)$ einigermaßen gleichmäßig, nach dem Differenzieren am Zielgerät eliminieren sie sich.
Das Signal am Zielgerät muss nicht mehr von der Masse aus gemessen werden, sondern kann zwischen den beiden Signalleitungen $V_O$ und $V_{O,inv)$ gemessen werden.

Der zweite Punkt hat einen großen weiteren Vorteil, dass man dadurch nicht die Massen der beiden Geräte miteinander verbinden muss. Das Verbinden der Geräte kann nämlich zu Masseschleifen führen. Mit dem Ground-Lift kappt man die Masseleitung zwischen den Geräten, wenn man es nicht erwünscht.

Bei Flex 500 wurde sowohl der symmetrische Eingang als auch der symmetrische Ausgang mit einem Ground-Lift-Schalter vorgesehen.

SPICE-Simulationsdateien zu den analogen Schnittstellen herunterladen

KiCAD-Schaltung und PCB-Design herunterladen

Analoge Lautstärkenregelung

7. Dezember 2019 / solocan / Noch kein Kommentar

Wir nehmen die Lautstärke logarithmisch wahr. Daher müssen wir die Lautstärkenregelung an den Geräten auch logarithmisch gestalten. Die digitale Umsetzung einer Lautstärkenregelung ist hier beschrieben. Bei der analogen Umsetzung einer Lautstärkenregelung gibt es u. a. folgende Möglichkeiten:

Logarithmischer Potentiometer (passive Regelung)
Aktive Lautstärkenregelung

Eine sehr verbreitete Schaltung zur aktiven Lautstärkenregelung ist das Baxandall-Regelung. Eine sehr gute Erklärung und Herleitung von dieser Regelung ist in dieser Publikation von TI beschrieben.

Umsetzung bei Flex 500

Beim Flex 500 wurde die Lautstärkenregelung von Baxandall folgendermaßen umgesetzt.

Die Übertragungsfunktion lässt sich als

(1) $\begin{equation*} \frac{V_O}{V_I}=-\frac{R_x}{R_{1-x}+\frac{1}{G}} \end{equation*}$

beschreiben, wobei $R_x$ und $R_{1-x}$ durch die Position des Potentiometer VR_VC1 resultierende Widerstände und $G$ die Verstärkung durch die zweite Stufe ist, in dem Fall $G=5$ .

Die SPICE-Dateien zur Lautstärkenregelung herunterladen

KiCAD-Schaltung und PCB-Design herunterladen

Flex 500 – Analog und DSP FX mischen

7. Dezember 2019 / solocan / Noch kein Kommentar

Das Mischen der Audio-Signale kann mit Summiererschaltungen von Opamps realisiert werden.

Die Summe $V_O$ von Eingangsspannungen $V_{1}$ und $V_2$ berechnet sich als

(1) $\begin{equation*} V_O=\frac{V_1 R_2+V_2 R_1}{R_1+R_2} [1+\frac{R_{f1}}{R_{f2}}] \end{equation*}$

Beim Flex 500 wird das Ausgangssignal vom internen DSP mit dem Analogsignal nach der Kompressionsstufe mit einem $R_P=10k$ Potentiometer gemischt, sodass

(2) $\begin{equation*} R_2=10k\Omega-R1 \end{equation*}$

ist.

LTSPice Mixersimulation herunterladen

KiCAD-Schaltung und PCB-Design herunterladen

Analoger Dynamikkompressor

7. Dezember 2019 / solocan / Noch kein Kommentar

Die Dynamikkompression (engl. Dynamic range compression) ist ein Prozess, der die Dynamik komprimiert bzw. reduziert. Das wird gemacht, indem die lauten Bereiche, die einen Schwellwert überschreiten, leiser gemacht werden, während die leiseren Bereiche unreduziert passieren. Die Charakteristik der Kompression lässt sich am Besten in einer Dynamikkurve darstellen, die die Beziehung zwischen der Einganglautstärke und Ausgangslautstärke beschreibt.

Die Steigung $\frac{b}{a}$ beschreibt die Kompressionsrate, mit der das Signal abgeschwächt wird. Dies greift ab dem Überschreiten eines Threshold-Werts.

Technische Beschreibung

Das Herzstück eines Kompressors ist ein spannungskontrollierter Verstärker (VCA). Im analogen Design, wird das mit komplexen Schaltungen realisiert. In der Digitaltechnik ist dies ein simpler Verstärkungsfaktor, mit dem das Signal multipliziert wird. In analoger Welt kann der VCA u. a. mit

Optokopplern (optische Kompressor)
diskreten Transistorschaltungen
integrierten Schaltkreisen

realisiert werden.

Der Verstärkungsfaktor wird in einem parallelen Pfad berechnet. Der parallele Pfad besteht aus einem Lautstärkendetektor (in der Regel realisiert mit Effektivleistung, RMS) und einer Logik, die die Reduktion aus der Lautstärke berechnet (Gain computer).

Loudness detector

Einer der wichtigsten Bestandteile einer Kompression ist die Berechnung der Lautstärke, Hier wird kontinuierlich ermittelt, wie hoch die empfundene Lautstärke ist. Gängigste Methode dafür ist der Effektivwert als quadratischer Mittelwert des relevanten Sampleabschnitts.

(1) $\begin{equation*} RMS=\sqrt{\frac{1}{n}\sum_{i=1}^{n}x_i^2} \end{equation*}$

Der RMS-Wert dient als Eingang für den Gain-Computer. Der Gain-Computer berechnet daraus die Verstärkung, die dem Signal appliziert werden soll. Es appliziert die Dynamikkurve, s. oben.

Parameter

Folgende Kontrollparameter sind für einen Kompressor Effekt üblich:

Input gain

Die Eingangsverstärkung wird auf das Eingangssignal appliziert, um das Signalniveau in einen gewünschten Platz in der Dynamikkurve zu platzieren. Alternativ kann man auch Threshold verschieben.

Threshold

Der Threshold (dt. für Schranke/Grenze) ist der Grenzwert, ab dessen Überschreitung eine Gain-Reduktion erfolgt, s. Diagramm.

Kompressionsrate

Sie beschreibt die Stärke der Gain-Reduktion nach Threshold, in der Dynamikkurve ist dies als Tangenzwert $\frac{b}{a}$ gezeigt.

Ab einem Wert von 60:1 wird von einem Limiter gesprochen.

Make-Up Gain

Der Gain-Computer appliziert eine Gain-Reduktion. Das bedeutet, die gesamte Lautstärke des Signals sinkt. Um das ältere Lautstärkenniveau zu erreichen, wird ein Make-Up Gain am Ausgang appliziert.

Soft-Knee / Hard-Knee

Ab dem Threshold ändert sich die Verstärkung, die man appliziert. Dieser Übergang, der in der Dynamikkurve oben scharf gezeichnet wurde, kann auch mild erfolgen. So dass die Gain-Reduktion langsam eintritt.

Attack

Der Attack-Wert bestimmt, wann die Gain-Reduktion nach einer Überschreitung eintreten soll. Sie liegt im Bereich von 5 bis 250 ms.

Release

Der Release-Wert bestimmt, wann nach einer Unterschreitung des Tresholds die Gain-Reduktion wieder aussetzen soll. Sie liegt üblicherweise im Bereich von 5 bis 100ms.

Analoge Implementierung

Bei Flex 500 wurde ein Kompressor auf Basis des integrierten Schaltkreises THAT4301 von THAT Corporation eingesetzt. Dieser beinhaltet

1x VCA
1x Loudness (RMS) detector
3x Opamps

und somit alles, was man für eine grundlegende Kompressorimplementierung braucht. Die Applikation und die Dimensionierung der externen Komponenten können dem Datenblatt entnommen werden.

Die Applikation für den Flex 500 sieht folgendermaßen aus:

Zudem existiert ein SPICE-Modell für den IC THAT4301, sodass man die Schaltung auch simulieren kann.

Kompressor Simulationsmodell für LTSpice herunterladen

Die gesamte KiCAD-Schaltung und das PCB Design ist verfügbar

KiCAD-Schaltung und PCB-Design herunterladen

Flex 500 – Analoger Equaliser / Tone stack

7. Dezember 2019 / solocan / Noch kein Kommentar

Der analoge EQ-Abschnitt besteht aus

Ein Tonestack mit zwei einstellbaren Kuhschwanzfiltern
- Low-Shelf
- High-Shelf
Drei parametrischen Equalisern
- Low-Mid-EQ
- Mid-EQ
- High-Mid-EQ

Die Schaltungskomponenten ist im folgenden gezeigt.

High-Low-Shelvingfilter Stack

Die Dimensionierung der Schaltung ist hier beschrieben.

Parametrischer Equalizer

Die Dimensionierung der Schaltungen ist hier beschrieben.

KiCAD-Schaltung und PCB-Design herunterladen

Author: solocan (page 2 of 8)

Mathematische Ansätze

Auto Korrelation

Ein effizienter Ansatz zur Frequenzbestimmung

Das Spektrum RASTERN

Erforderliche Sample-Anzahl für die Raster berechnen

Auto-Korrelationswert berechnen

Auto-Korrelationswert normieren

Extrema des Spektrums (PEAKS) ermitteln

Nach den exakten Frequenzen (Offsets) suchen

Stochastische Abschätzung der GESUCHTEN Frequenz

Ressourcen

Systemarchitektur

Codec

SAI

DMA

Puffer

Zustandsmaschine

Implementierung

Board-Design

Analoge Ein- und Ausgänge

Oszillator

Ressourcen

Board-Design

Symmetrische Eingänge

Symmetrische Ausgänge

Digitale Schnittstellen

Initialisierungssequenz

Oszillator

Ressourcen

Kopfhörerausgang

Symmetrischen Eingang

Symmetrischer Ausgang

Ground lift

Umsetzung bei Flex 500

Technische Beschreibung

Das Herzstück eines Kompressors ist ein spannungskontrollierter Verstärker (VCA). Im analogen Design, wird das mit komplexen Schaltungen realisiert. In der Digitaltechnik ist dies ein simpler Verstärkungsfaktor, mit dem das Signal multipliziert wird. In analoger Welt kann der VCA u. a. mit

Loudness detector

Parameter

Input gain

Threshold

Kompressionsrate

Make-Up Gain

Soft-Knee / Hard-Knee

Attack

Release

Analoge Implementierung

High-Low-Shelvingfilter Stack

Parametrischer Equalizer

Erforderliche Sample-Anzahl $n$ für die Raster berechnen