Hierbei wird eine Solltrajektorie konstruiert und die Lagegrößen des Roboters, also Position und Orientierung, auf diese Solltrajektorie geregelt. Die Regelung erfolgt im Folgenden mit einem PD-Regler, da das integrale I-Glied durch die Addierung der differentiellen Bewegungen bereits mitbeinhalten ist und die Fehler der Lagegrößen sich summieren. Ein typischer Regelkreis sieht wie in der Abbildung 1 aus.

Das Diagramm stellt einen typischen Regelkreis mit Rückführung dar. Hierbei stellt der Regler anhand der Einganggröße Regelabweichung ![]() die Stellgröße
die Stellgröße ![]() . Hierbei ist die Regelgröße die IST-Position des Roboters
. Hierbei ist die Regelgröße die IST-Position des Roboters
(1) 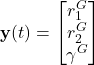
und die Führungsgröße die Soll-Position, also die Soll-Trajektorie
(2) 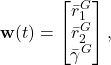
die der Roboter nachfahren muss. Daraus ergibt sich der Messfehler
(3) ![]()
Die Regelgleichung des idealen PD-Reglers im Zeitbereich kann dann als
(4) ![]()
formuliert werden, wobei der Vektor ![]() der Verstärkungsvektor und der
der Verstärkungsvektor und der ![]() die Zeitkonstante ist, die das D-Glied parametrisiert. Die Stellgrößen, die hierbei eingestellt werden, sind die Spannungen der beiden Motoren
die Zeitkonstante ist, die das D-Glied parametrisiert. Die Stellgrößen, die hierbei eingestellt werden, sind die Spannungen der beiden Motoren
(5) ![]()
Der ideale PD-Regler genügt hierbei nicht ganz den Anforderungen, da das reale System sowohl software- als auch hardwareseitige Verzögerungen aufweist. Wenn man ein PT-Glied in den PD-Regler integriert, erhält man
(6) ![]()
wobei die Matrix ![]() für die Verzögerungszeitkonstante steht. Die Bewegungsgleichungen des Roboters lassen sich i.a. als
für die Verzögerungszeitkonstante steht. Die Bewegungsgleichungen des Roboters lassen sich i.a. als
(7) ![]()
schreiben, wobei ![]() die Massenmatrix,
die Massenmatrix, ![]() die Dämpfungsmatrix,
die Dämpfungsmatrix, ![]() Steifigkeitsmatrix und
Steifigkeitsmatrix und ![]() die Matrix der äußeren Kräfte sind. Um die Bewegungsgleichungen als differentielle Gleichungen ersten Grades zu beschreiben, werden diese im Zustandraum dargestellt. Die Zustandsgleichung lautet i.a.
die Matrix der äußeren Kräfte sind. Um die Bewegungsgleichungen als differentielle Gleichungen ersten Grades zu beschreiben, werden diese im Zustandraum dargestellt. Die Zustandsgleichung lautet i.a.
(8) ![]()
Mit dem Zustandvektor
(9) ![]()
und dem erweiterten Kraftvektor
(10) ![]()
lassen sich die Systemmatrix ![]() als
als
(11) ![]()
und die Eingangsmatrix ![]() als
als
(12) ![]()
formulieren. Im konkreten Fall des Roboters bietet sich die Vereinfachung an, bei der Ermittlung der Massenmatrix die Form als Zylinder anzunehmen. Die Dämpfungsmatrix, sowie die Steifigkeitsmatrix wurden emprisch ermittelt.
Ausblick: Die Parameteroptimierung für den Regler wurde noch nicht methodisch durchgeführt und ist ein anstehender Punkt im Roadmap.
