Das Kammfilter ist ein Frequenzfilter, das das verzögerte Signal zum nichtverzögerten Signal mischt und dadurch bestimmte Frequenzen auslöscht. (Kammeffekt). Im Grunde ist das Kammfilter eine Verzögerungslinie mit Rückkopplung.

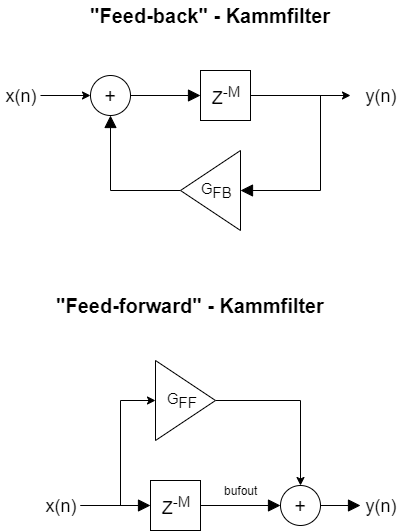
Die diskrete Übertragungsfunktion H(z) eines Feedback-Kammfilters M-ter Ordnung kann als

(1) $\begin{equation*} H(z)=\frac{z^{-M}}{1-G_{FB}z^{-M}} \end{equation*}$

beschrieben werden.

Kammfilter mit Tiefpass

Man kann die Rückkopplung nur auf bestimmte Frequenzen begrenzen, in dem man ein Frequenzfilter in die Rückkopplungsbahn einbaut. Das ist für Reverb-Implementierung wichtig, da in der Realität die Schallenergie der höheren Frequenzen schneller abgedämpft wird. Um dies nachzubilden, kann ein Tiefpassfilter erster Ordnung eingebaut werden:

(2) $\begin{equation*} H_{LP}(z)=\frac{1-d}{1-d z^{-1}} \end{equation*}$

oder noch einfacher eine Glättung:

(3) $\begin{equation*} H_{LP}(z)=\frac{1}{1-d z^{-1}} \end{equation*}$

Wird dies in die Rückkopplungsbahn integriert, sieht es folgendermaßen aus:

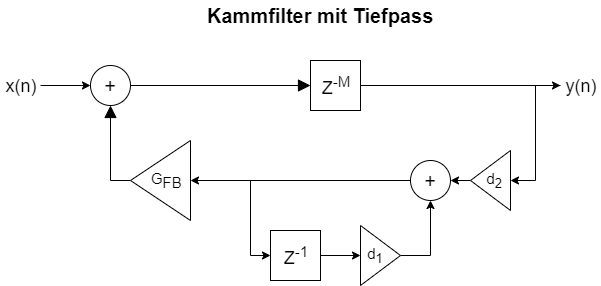
Hierbei wurden zwei Dämpfungskoeffizienten $d_1$ und $d_2$ hinzugefügt.

Implementierung

Die Implementierung des Kammfilters mit Tiefpass ist im Folgenden gezeigt:

/*
Main process comb filter with low pass
*/
float c_comb::process(float x){

	float y;

	y = buffer[cptr];

	filterstore = (y*damp2) + (filterstore*damp1);

	buffer[cptr] = x + (filterstore*feedback);

	if(++cptr>=bufsize) cptr = 0;

	return y;
}

Main process comb filter with low pass

float c_comb::process(float x){

float y;

y = buffer[cptr];

filterstore = (y*damp2) + (filterstore*damp1);

buffer[cptr] = x + (filterstore*feedback);

if(++cptr>=bufsize) cptr = 0;

return y;

}

Can Kosar

Digitales Tiefpass-Kammfilter

Kammfilter mit Tiefpass

Implementierung

Schreibe einen Kommentar Antworten abbrechen