Ein Rotary-Effekt ist ein Modulationseffekt, der die Frequenz bzw. die Tonhöhe (Pitch) des Eingangssignals mit einem Niedrigfrequenzoszillator (LFO: engl. Low-frequency oscillator) ändert. Somit entsteht eine Rotary bzw. je nach Parametrierung ein Vibrato-artiger Effekt.
Er ist sehr ähnlich zum Chorus-Effekt mit dem Unterschied, dass hierbei das Signal nicht kopiert wird sondern das trockene Signal verarbeitet wird: Ohne Kopieren und zurückmischen. Daher resultiert hierbei kein Phasenauslöschungseffekt.
Im folgenden ist das Grundprinzip des Rotary-Effekts aufgezeigt.
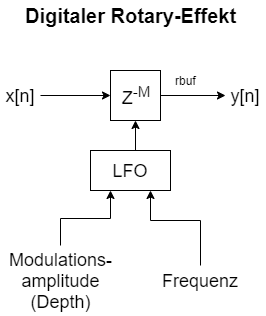
Parameter
Folgende Kontrollparameter sind für einen Flanger-Effekt üblich:
Frequenz
Mit der Frequenz kontrolliert man die Geschwindigkeit der Frequenzmodulation. Üblicherweise in Hertz [Hz]. Typische Werte zwischen 1Hz und 25Hz.
Tiefe (Depth)
Mit diesem Parameter kontrolliert man die Wirksamkeit der Modulation. Sie wird in Prozent oder in Millisekunden (Delay-Zeit) angegeben. Wenn z.B. die Basis-Delayzeit 25ms ist und die Tiefe 50%, dann bedeutet das, dass das Delay zwischen 12,5ms und 37,5ms moduliert wird.
Modulation mit LFO
Ein LFO ist nichts anderes als ein Signalgenerator, der in der Regel ein niederfrequentes Sinus-Signal generiert. Diese Signalquelle nutzt man u. a. zur Modulation eines Signals.
Im Fall eines Rotary-Effekts moduliert man „die Abtastfrequenz“. Konkret tut man das, in dem man die Delay-Zeit kontinuierlich erhöht und reduziert. Diese Delay-Zeit ist in der Regel sehr kurz und liegt im Fall von Chorus in der Regel 5-50ms. Man nimmt eine Referenzdelayzeit. Z.b. 20ms und moduliert diese mit LFO zwischen 10ms und 30ms. Dadurch verlangsamt und beschleunigt das Signal und es entsteht eine Frequenzverschiebung.
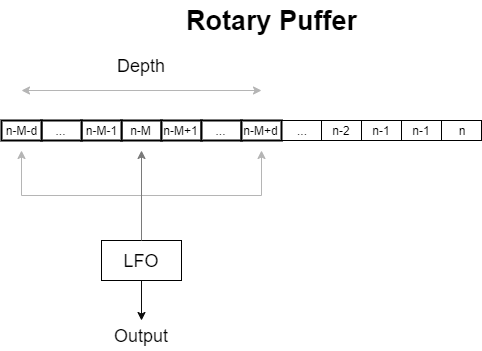
Implementierung
LFO
Für das Rotary-Puffer wird ein Kreispuffer benötigt, in dem Eingangssignal aufgenommen wird.
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 |
/* LFO */ float c_rotary::lfo(void){ float y_lfo; //Calculate LFO value y_lfo=sin(a_lfo); //Update angle a_lfo+=a_step; if(a_lfo>=2*PI){ a_lfo=a_lfo-2*PI; } return y_lfo; } /* Calculate rotating delay */ float c_rotary::get_current_delay(void){ //Calculate time float t; t=d_base+depth*lfo(); //Return the delay time return t; } |
Hauptroutine
Der Algorithmus vom Rotary-Effekt ist vergleichbar mit einem Chorus-Algorithmus ohne Signalkopie und Trockensignal / Effektsignal-Mischung.
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 |
/* Rotary main routine */ float c_rotary::process(float x){ float y; float t_c; //Current delay //Get current delay t_c=get_current_delay(); //Delay time //Calculate the position of the pointer int wptr; wptr=rptr-rint(t_c*FSms); if(wptr<0){ wptr+=rotary_len; } //Calculate output y=rbuf[wptr]; //Update the buffer rbuf[rptr]=x; //Increment rptr++; if(rptr>=rotary_len){ rptr-=rotary_len; } return y; } |
Klangbeispiele
Anbei ist dieser Algorithmus mit ein paar verschiedenen Parametern zu hören.

Schreibe einen Kommentar